Section III.5
Section
III.5 Shear
Flow
Analysis for
Unsymmetric
Beams
In chapter II, a general equation for the bending stress was
introduced. It was further shown that this equation could be used on any
cross section, symmetric or unsymmetric, under symmetric or unsymmetric
bending moment.
There is a similar general equation for shear flow.
It too can be used for any cross section, symmetric or
unsymmetric, under symmetric or unsymmetric transverse shear force.
This equation is derived from Eq. (II.1), and is
given as
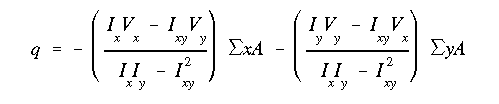
When the section is symmetric there will be no product of inertia, and if only
a vertical shear force is applied, this
equation reduces to what we have used previously for determining shear flow
distribution at a given section.
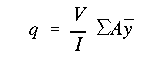
The analysis procedure for unsymmetrical cross sections is as follows:
- Determine, as needed, the centroid, moments of inertia, and the
shearing load in the problem.
- Consider the two parts of the general shear flow equation separately.
- Determine the shear flow resulting from each part.
- Combine the two parts together to get the final shear flow distribution.
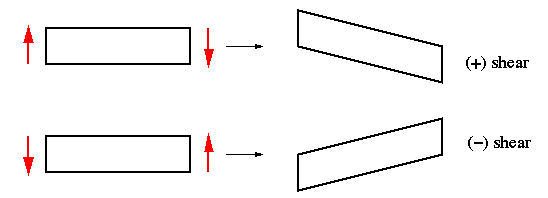
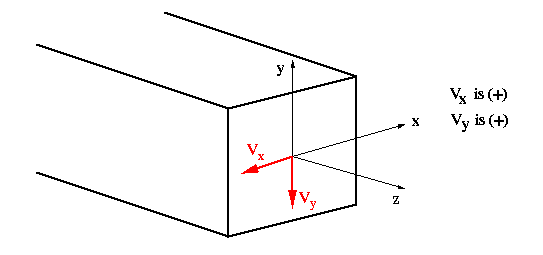
When using this equation, it is
important to consider the 'signs' on the transverse shear force components, Vx
and Vy. The sign convention used is as follows:
EXAMPLE
PROBLEMS
- Example 1 Shear flow distribution,
shear center location, and max shear stress calculation of a transversely loaded
beam with an L cross section
 To Section
III.6
To Section
III.6
 To Section
III.4
To Section
III.4
 To Index Page of
Transverse Shear Loading of Open Sections
To Index Page of
Transverse Shear Loading of Open Sections
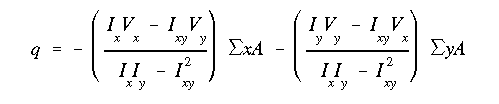
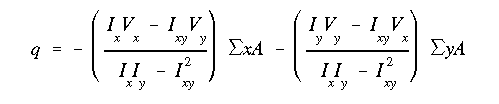
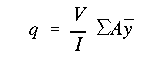


 To Section
III.6
To Section
III.6 To Index Page of
Transverse Shear Loading of Open Sections
To Index Page of
Transverse Shear Loading of Open Sections