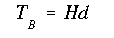
To better understand this behavior let's consider a thin-walled bar, with an "I" cross section, fixed at one end and free at the other where a torque is applied. In the vicinity of the fixed end the upper and lower flanges of the bar act as short beams, therefore, have considerable bending stiffness, and prevent the cross section from warping under the applied torque. Hence, the torque is carried mainly in the form of transverse shear in these flanges. As a result the upper and lower flanges deflect laterally in opposite directions - referred to as differential bending. In this case, the torque can be represented by a couple of force H acting in each flange
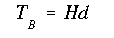
At the other extreme point, near the free end, the applied torque is carried mainly in the form of torsional shear or pure shear as the cross section is free to warp. This is because, near the free end, the flanges are basically long beams with less bending stiffness, therefore, shear rigidity dominates in this case.
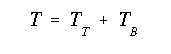
For angle of twist due to torsion in (a), from the analysis in section A6.6, we can write
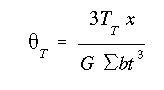
where the length of each rectangular portion of the cross section is assumed to be much greater than its thickness.
For angle of twist due to torsion in (b) we use the relationship between the lateral deflection of the flanges and the angle of twist as
Now, from mechanics of materials we can relate the flange deflection to transverse shear force H in the flange as
Combining the pevious equations we determine angle of twist
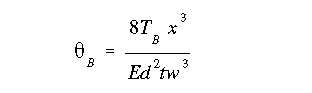
Since the two angles of twist are equal, the right hand sides of the two equations can be set equal to determine the ratio between the portion of the torque taken up by transverse shear and portion taken up by pure shear.
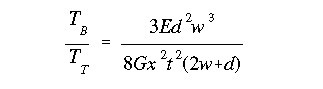
 To Section
I.10
To Section
I.10
 To Index Page of
Pure Torsion
To Index Page of
Pure Torsion