Structural Analysis II Section A6.4
Section
I.2 Torsion of
Non-Circular
Bars
The observations made for torsion of members with circular cross sections
do not
hold for those with non-circular cross sections. Consider the following facts
for members with non-circular cross sections:
- The shear stress is not constant at a given distance from the
axis of rotation. As a result sections perpendicular to the axis of member warp,
indicating out-of-plane displacement.
- The theory of elasticity shows that the shear stress at the corners is
zero.
- Maximum shear strain and stress are not
at the farthest distance from the rotational axis of a homogeneous
non-circular member.
Members with rectangular cross sections:
For a rectangular member under torsion the corners do not
distort; the corner square angles remain square after torque is
applied. This indicates that shear strain is zero at the
corners since there is no distorsion. This fact is illustrated in this
figure.
St. Venant was the first to accurately describe the shear
stress distribution on the cross section of a non-circular member
using the Theory of Elasticity. For more information click here.
Theory of Elasticity shows that:
- the maximum shear strain and stress occur at the centerline of the
long sides of the rectangular cross section
- the shear strain and stress at the corners and center of the rectangular
cross section are zero.
- the strain and stress variations on the cross section are primarily
nonlinear.
- the preceding statements are demonstrated in the following
figure.
The theory of Elasticity has been applied to find analytical
solutions for the torsion of rectangular elastic members. The resulting equations for shear stress and angle of twist are as follows:
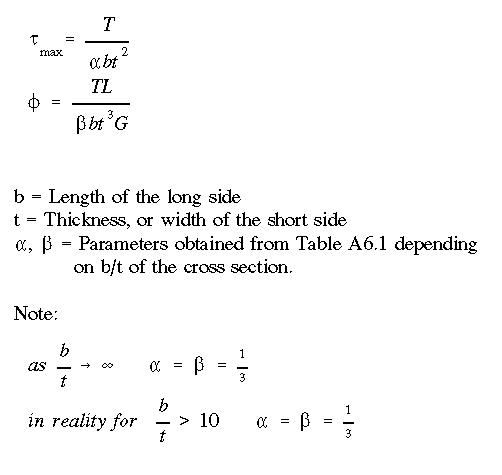
Here is Table A6.1
NOTE: The equations described in this section can only be used for
members having OPEN
cross-sectional shapes. For open cross sections composed of multiple thin plates
refer to Section I.5.
 To Index Page of
Pure Torsion
To Index Page of
Pure Torsion
 To Section
I.1
To Section
I.1
 To Section
I.3
To Section
I.3
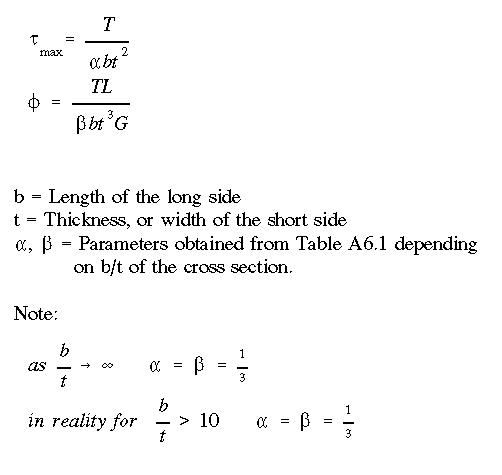
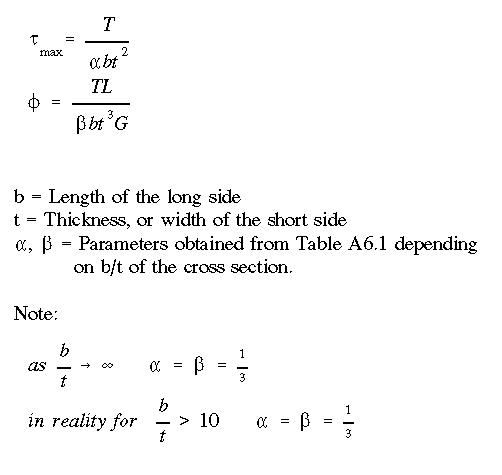
 To Index Page of
Pure Torsion
To Index Page of
Pure Torsion
 To Section
I.1
To Section
I.1
 To Section
I.3
To Section
I.3