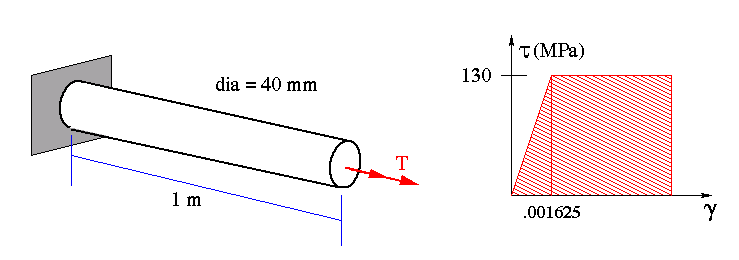
Problem Data:
Left end is fixed.
T is applied at the tip of the shaft.
Length = 1m, Diameter = 40 mm
max. elastic shear stress = 130 MPa,
max. elastic shear strain = .001625

Answers:

(a) T = 1,633.63 N-m, angle of twist = 4.66 degrees
(b) r (elastic rim) = .0178 m, angle of twist = 5.23 degrees
(c) permanent twist angle = 0.11 degrees

2. The non-homogeneous circular shaft shown is composed of a steel core bonded perfectly to an aluminum tube with the properties shown in the stress-strain diagram.

(a) Determine the maximum elastic torque that can be carried by the non-homogeneous shaft.
(b) Determine the minimum torque required to make only the aluminum tube fully plastic.
(c) Sketch the shear strain distribution versus the radius for parts (a) and (b) with the interface and maximum values well defined.
(d) Sketch the shear stress distribution versus the radius for parts (a) and (b) with the interface and maximum values well defined.

Problem Data:
radius of the steel core = 0.5"
radius of the aluminum shell = 1"
shear rigidities shown on the figure.

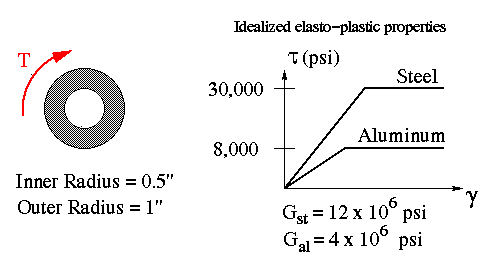
Answers:

(a) T = 14,137.2 in-lb
(b) T = 19,373.2 in-lb
(c) shear strain at interface = .001 (for part a) and .002 (for part b)
(d) shear stress at interface = 12,000 psi in steel and 8,000 psi in aluminum (for part a) and 24,000 psi in steel and 8,000 psi in aluminum (for part b)

3. For the thin-walled extruded "Z" section having a length of 96 in, determine
(a) the maximum shear stress and its location,
(b) the corresponding angle of twist.
(c) If the stringer is fixed at one end, determine the value of TB, TT and angle of twist at 12 in from the fixed end. Use the weighted average thickness of .0675 in.

Problem Data:
Left end is fixed.
T = 100 in-lb, E = 10 Msi, G = 4 Msi
Top flange: length = 3 in, thickness = .05 in,
Web: length = 6 in, thickness = .1 in,
Bottom flange: length = 3 in, thickness = .02 in

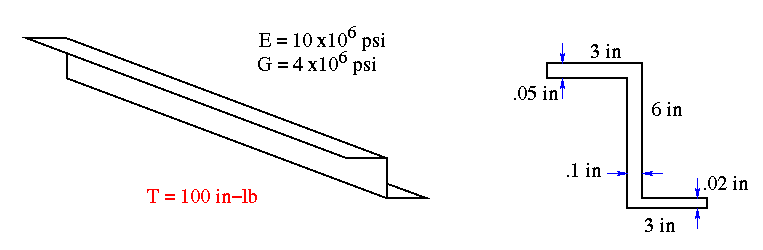
Answers:

(a) max. shear stress = 4,688.23 psi at the middle edge of the web
(b) angle of twist = 64.47 degrees
(c) TT = 0.86 in-lb, TB = 99.14 in-lb, angle of twist = 0.1 degrees

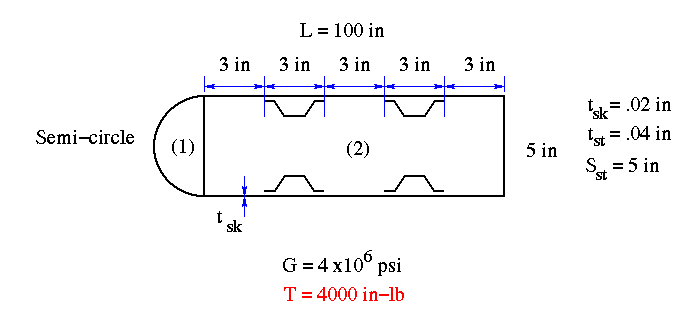
4. Consider the two-cell stiffened wing section shown, determine
(a) the shear flow distribution,
(b) the shear stress distribution,
(c) the angle of twist at the free end.

Problem Data:
First cell on the left: semicircle of radius = 2.5 in
Second cell on the right: rectangle of dimensions 15 in x 5 in.
T = 4000 in-lb, G = 4 Msi,
length = 100 in, tsk = .02 in, tst = .04 in, Sst = 5 in.

Answers:

(a) q1 = 16.4 lb/in, q2 = 24.5 lb/in
(b) shear stress along the semi-circular web = 819.75 psi
(c) angle of twist = 0.32 degrees

To Index Page of Pure Torsion