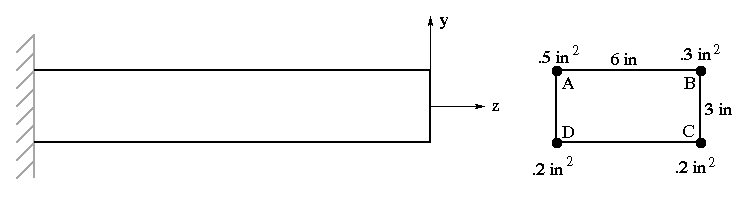
1. Consider the cantilever box beam shown below. Assuming the entire skin is ineffective in bending, for Mx = 100,000 in-lb, determine
(a) the normal stresses in stiffeners A, B, C, and D,
(b) the location and orientation of neutral axis.

Answers:
(a)
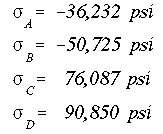
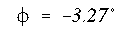
(b) The neutral axis passes through the centroid of the section and is along
the x axis.
2. For the stiffened thin-walled section and loading shown, determine
(a) the location of neutral axis,
(b) the normal stress in stiffener A only.
Assume the entire skin is ineffective in bending.
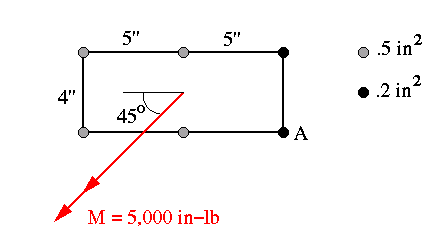
Answers:
(a) Neutral axis passes through the centroid of the section with
orientation of NA = 17.1 degrees
(b) Normal stress in stiffener A = 1,443.7 psi
3. Consider the composite (non-homogeneous) rectangular beam shown. For an elastic bending moment of Mo = 100,000 in-lb, determine
(a) the maximum bending stress in steel section,
(b) the maximum bending stress in aluminum section.
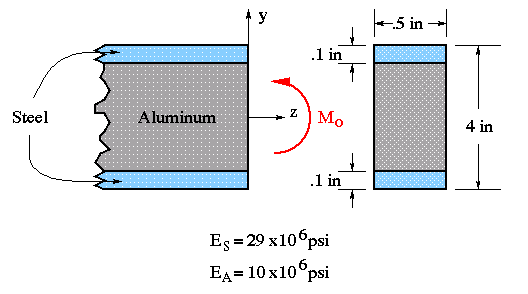
Answers:
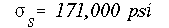
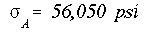
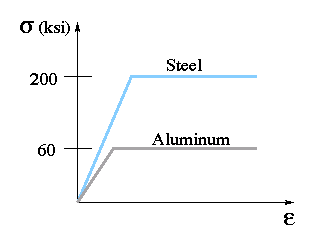
4. Using the same composite beam as in problem 3, and considering the stress-strain diagram shown, determine the maximum (i.e., fully plastic) bending moment which can be applied on the beam.
Answers:
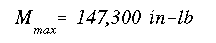
5. Consider the aluminum channel section with two titanium-alloy plates perfectly bonded to the top and bottom flanges as shown in the figure. For the horizontally applied bending moment,
(a) determine the maximum elastic bending moment, and sketch the location
of neutral axis.
(b) Sketch the normal strain and stress distributions corresponding to part (a)
with interface and max values well defined.
(c) Explain clearly, based on the context of non-homogeneous beam bending, why
we would want to attach the titanium plates to the aluminum channel.
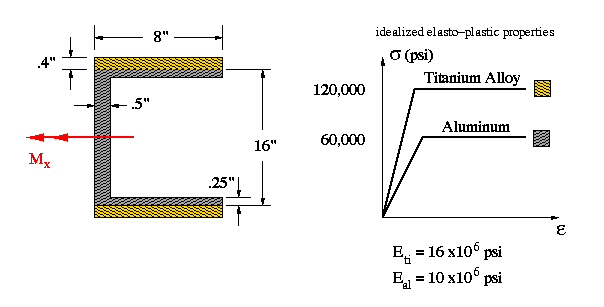
Answers:
(a) Mx = 8,189,392 in-lb, with orientation of neutral axis = 0 degree
(a) the value of max. elastic moment, and sketch the corresponding N.A. position,
(b) the value of moment necessary to produce a max. normal strain of .003, and
sketch the corresponding N.A. position.
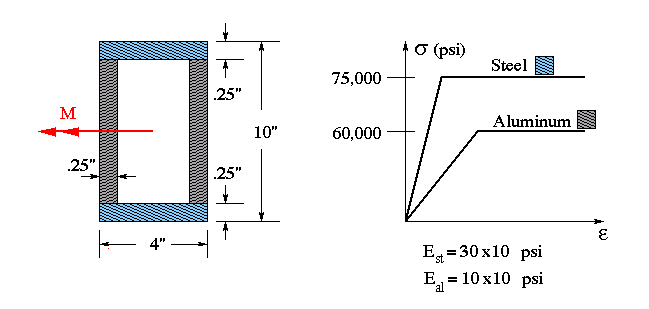
Answers:
(a) M = 891,744,8 in-lb, corresponding to max. strain = .0025
(b) M = 945,593.8 in-lb, corresponding to max. strain = .003
 To Index Page of
Pure Bending
To Index Page of
Pure Bending