SectionIII.3 example 1

SectionIII.3 example 1 SHEAR STRESS COMPONENTS t_yx and t_zx

The T section shown below is used to explain the difference between the two components of shear stress, i.e., t _yx and t_zx. Let's assume that the transverse shear force is along the y axis (passing through the shear center of the section) and that V_y = 1000 lb.

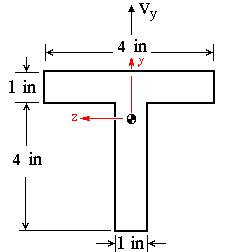
SOLUTION:

With the shear force along the y axis, the average flexural shear stress formula for the two components of interest is written as

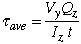
Although the general form of the equation is the same for both components, there is a difference in the way Q_z and t are found in each case. With V_y given, we proceed with the calculation of centroidal position.

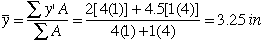
The centroid is located at 3.25 in. from the bottom edge of the section. The moment of inertia about the z axis is found as

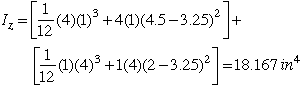
To calculate the t_yx component of shear stress, the longitudinal surface has to have a normal in the y direction. The intersection of this longitudinal surface and the transverse surface is shown by a solid blue line in the figure below.

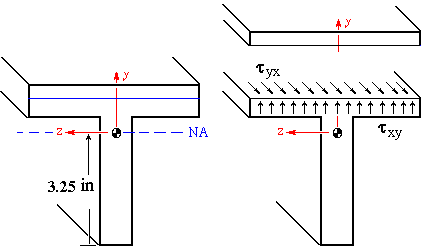
Depending on the position of the longitudinal surface along the y axis, the corresponding value for Q_z is found as

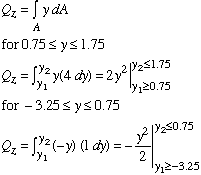
The equation for Q_z is quadratic. Q_{z_max} = 5.28 in³, and it occurs at the NA (y₂ = 0). The variation of Q_z is shown below.

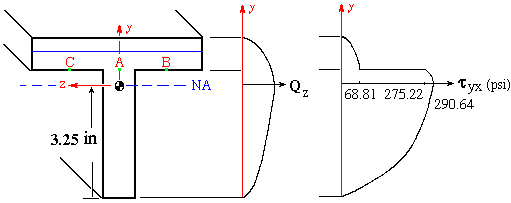
With the variation of Q_z known, t_yx is found as

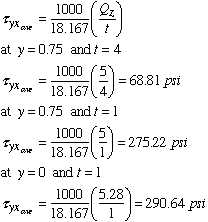
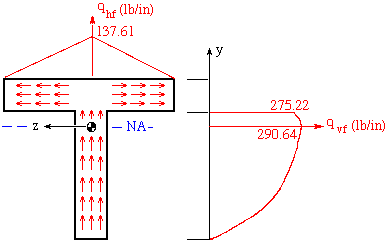
Keep in mind that t is the width of the longitudinal surface. Along -3.25 < y < 0.75, t = 1 in. and along 0.75 < y < 1.75, t = 4 in. As is shown in the figure above, there is a discontinuity in the shear stress at y = 0.75 in. due to the discontinuity in t. The maximum value of t_yx is found to be 290.64 psi and it occurs at the NA. The values of t_yx over the longitudinal surface are equal in magnitude to the corresponding t_xy values on the transverse surface.

It is crucial to pay attention to t_yx variation at the junction. The value of 68.81 psi found in the analysis refers to the shear stress in the horizontal flanges just above the junction point. As there can be no shear stress on a free surface, the shear stress t_yx and its counterpart t_xy are zero at points B and C but not at point A. As indicated by its plot, t_yx is more significant in the vertical flange as opposed to horizontal flanges.

To calculate the t_zx component of shear stress, the longitudinal surface has to have a normal in the z direction. The intersection of this longitudinal surface and the transverse surface is shown by a solid blue line in the figure below.

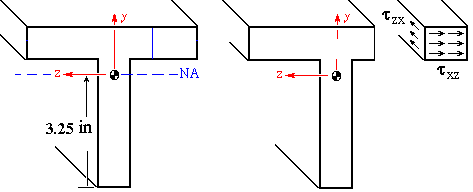
Depending on the position of the longitudinal surface along the z axis, the corresponding value for Q_z is found as

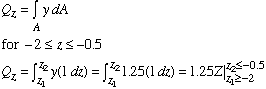
The equation for Q_z is linear in this case. At the section intersecting the corner of the horizontal and vertical flanges i.e., z_z = +/-0.5, Q_z = 1.875 in³. The variation of Q_z is shown below.

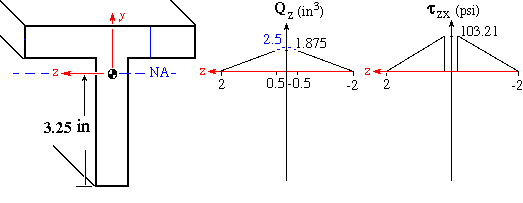
The blue dashed line gives the Q_z variation at the junction of the horizontal and vertical flanges. This value is used to find the shear flow at that location.

With the variation of Q_z known, t_zx is found as

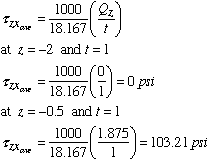
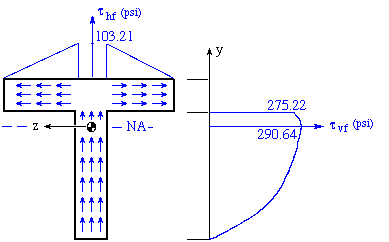
Keep in mind that t is the width of the longitudinal surface. Along -2 < z < -0.5, t = 1 in. As is shown in the figure above, t_zx reaches its maximum value of 103.21 psi in the horizontal flanges at the junction with the vertical flange. In the vertical flange this component of shear stress is zero as shown below.

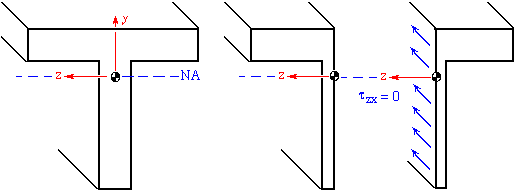
Notice that there is a counterpart shear stress (t_xz) on the transverse surface. Also in this case t_zx is more significant in the horizontal flanges as opposed to the vertical flange.

key observation:

At any point on the boundary the resultant shear stress is parallel to the boundary. This fact helps us to sketch the figures shown below as a general depiction of shear flow and shear stress variations in this example.

To Section III.3

To Index Page of Transverse Shear Loading of Open Sections