Section A3.10 example 1

Section A3.10 example 1 SECTION A3.10 EXAMPLE 1

For the cross section shown, determine the

(a) moment of inertia about the horizontal centroidal axis, x

(b) moment of inertia about the vertical centroidal axis, y

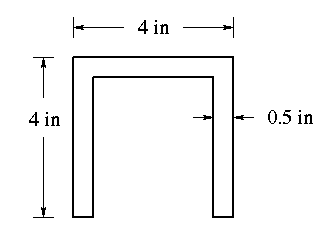
EQUATIONS USED

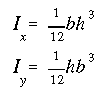
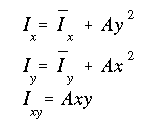
SOLUTION

The cross section is broken up into separate section.

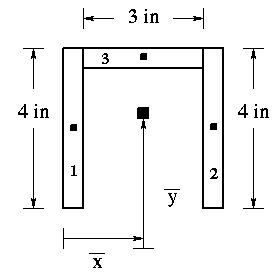
The centroid of the cross section is located at: Note that (2.5) in xbar equation should be (0.25). The final answer for x bar is correct, however.

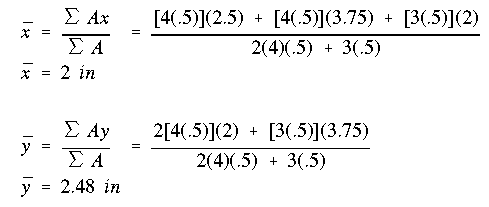
The moments of inertia for each rectangular section are

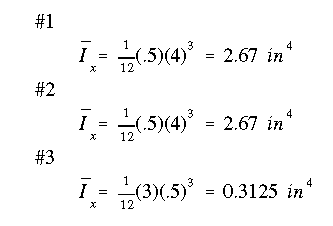
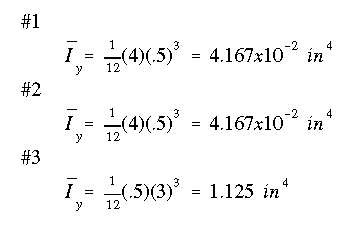
(a) Now, using the parallel axis theorem, we calculate the moment of inertia of the entire cross section about the horizontal x axis:

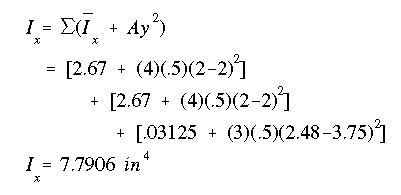
'y' is the distance from the centroid of the cross section to the centroid of each particular rectangle.

(b) Now, using the parallel axis theorem, we calculate the moment of inertia of the entire cross section about the vertical y axis:

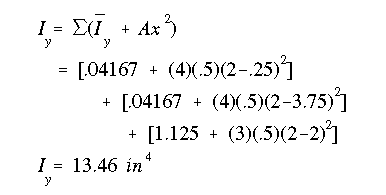
'x' is the distance from the centroid of the cross section to the centroid of each particular rectangle.

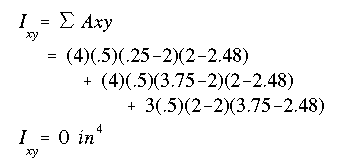
'x' and 'y' terms in this equation are the same as those defined above. Note that the product of inertia is zero as the cross section has one axis of symmetry, i.e., the y axis.

To Section A3.10

To Index Page of Pure Bending