EQUATIONS USED
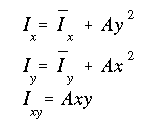
SOLUTION
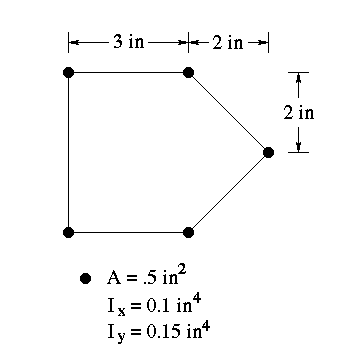
This is a lumped area cross section. Unless otherwise stated, the moment of inertia of the skin can safely be ignored, this leaves only the moment of inertia due to the lumped areas.
Often the actual moments of inertia for the individual lumped areas are not given. This is because the first component in the parallel axis theorem, in comparison to the second, is very small in such configurations.
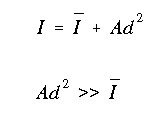
To demonstrate this, the moment of inertia will be found using the complete equation, then found by ignoring the first component of the parallel axis theorem.
With respect to the bottom left stringer, the centroid is located at
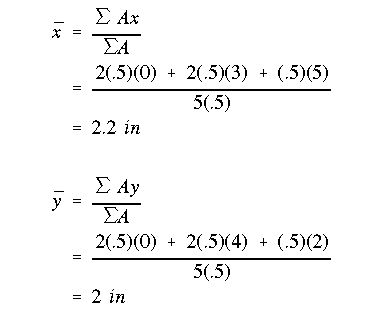
The complete moments of inertia are:
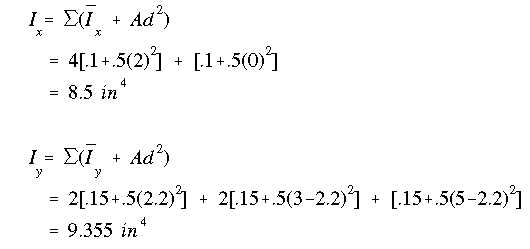
Now by just using the second component in the parallel axis theorem, we get
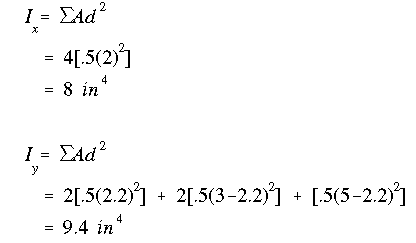
The error in Ix is 5.9% and that in Iy is 0.5%. In a real situation the difference is around 0.5%.
The product of inertia is
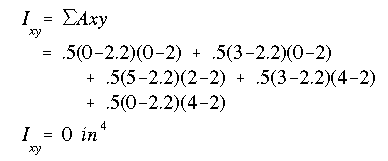
As expected, the product of inertia is zero because of symmetry.
 To Section A3.10
To Section A3.10
 To Index Page of
Pure Bending
To Index Page of
Pure Bending