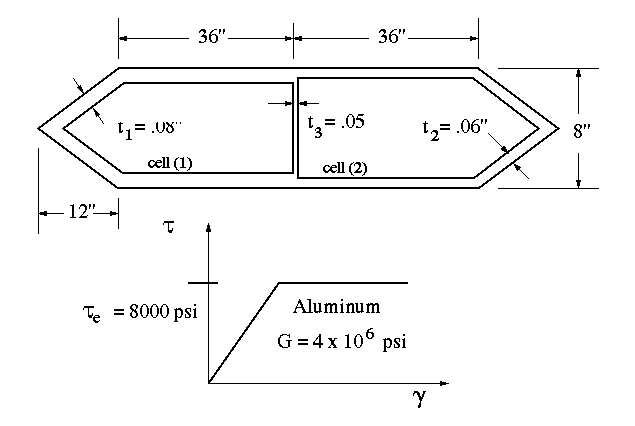

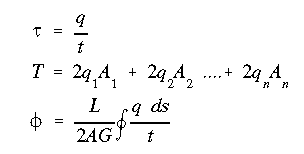
(a) First, write the torque equation.
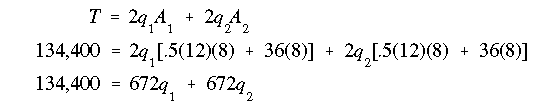

So far we have obtained one equation in two unknowns. To solve for the two unknowns we need a second equation in terms of the same two unknowns. We use the angle of twist relationship, that is the twist of both cells is the same. Writing the angle of twist equation for both cells and setting them equal to each other gives
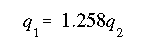
Now by substituting this relation into the torque equation we can solve for q1 and q2, and by taking the difference between these two shear flows we can obtain q3 to be
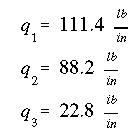
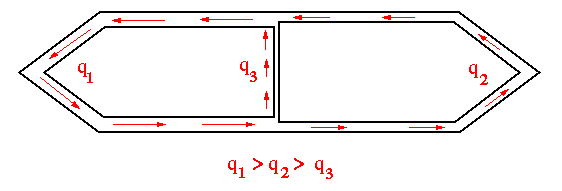
NOTE: q3 was determined by subtracting q2 from q1, hence, positive value for q3 indicates that this shear flow is in the same direction as q1, which in this problem is found to be counter-clockwise.
(b) The shear stress along each web is constant, and is equal to the shear flow along the web divided by the web thickness. There are three different web thicknesses and three different shear flows, hence, there will be three different shear stresses
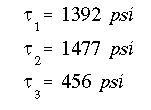
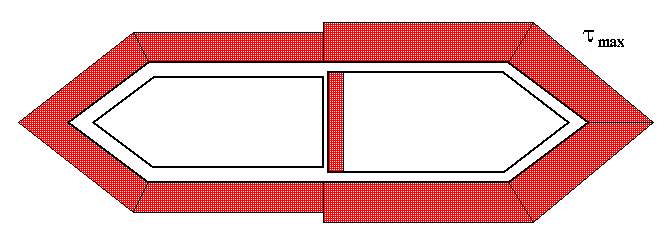
NOTE: The maximum shear stress occurs in the web which has the maximum q/t value and not necessarily minimum t. As can be seen in this example, the interior web has the minimum thickness, but not the maximum stress. This is obviously because, unlike single-cell sections, the shear flow is not constant everywhere.
Compared to example 1 in section A6.8, the maximum shear stress is in the same place, but it is smaller. In this case the interior web relieved the shear stress carried in wall (2), and increased the stress in wall (1), while reducing the overall angle of twist. The conclusion that can be drawn is that the presence of interior wall increases the torsional stiffness of the thin-walled sections.
(c) Substituting the values of the shear flows back into the angle of twist equation gives
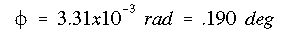
Suggested Exercise:
Rework this example problem by letting t1 = t2 = .06 in., and examine the changes in the results.
 To Section A6.10
To Section A6.10