Section I.1 example

SECTION I.1 EXAMPLE

Stepped bar ABC is made of Aluminum alloy with section AB filled with steel. Use the properties given to do the following:

Use the Java applet below to change the input data and see the corresponding results

EQUATIONS USED

SOLUTION

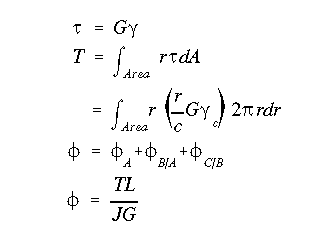
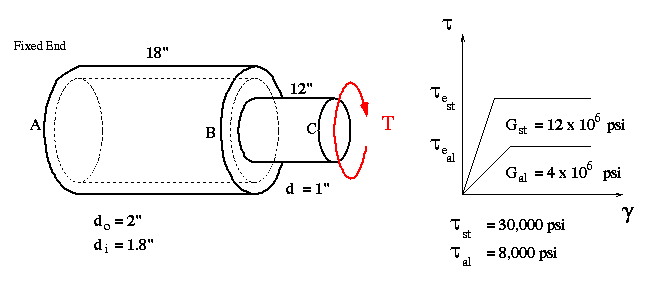
(a) This problem is an example of circular shafts with material and/or geometric discontinuities along the axis. Such axial discontinuties require that the shaft be broken up into several parts such that in each part we have uniform axial properties and constant loading. In this example we have material and geometric discontinuties but not loading discontinuity as torque is equal to T everywhere along the shaft. Notice also while portion BC is homogeneous (made of aluminum only), portion AB is not. Thus, to analyze this problem we use elastic torsion formula for portion BC and the general torsion formula (integral form) for portion AB.

First, we find the maximum elastic torque that portion BC can carry. It will correspond to the maximum elastic shear stress and maximum shear strain in this section - both at the surface in this case. From the stress-strain curve in the figure, we know the maximum elastic shearing stress for aluminum is 8000 psi. Using Hooke's law, the maximum elastic shear strain (the strain at radius 'c') can be found

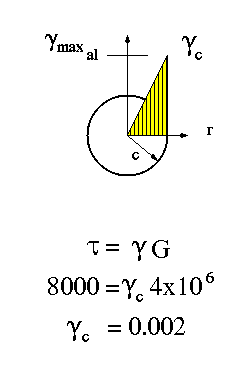
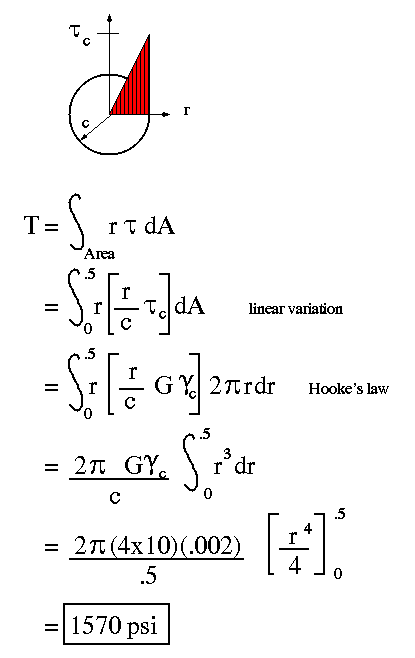
Now using the elastic torsion formula, the maximum elastic torque for section BC is

Notice that this is not the final answer yet because this torque may be greater that the maximum elastic torque for portion AB.

Now find maximum allowable torque for portion AB. The maximum strain will be at the surface as before. Since the shell is aluminum, the maximum strain will be the same as above

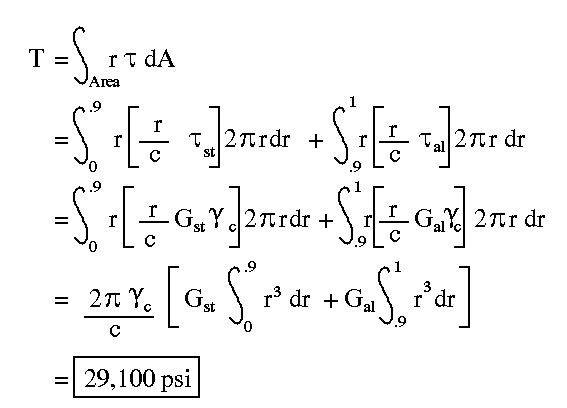
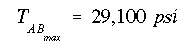
Using the torque equation above, the maximum allowable torque for portion AB is

Therefore, the maximum elastic torque for the shaft so that both portions AB and BC remain elastic will be

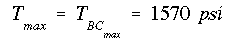
Please note that the unit for torque should be in-lb instead of psi.

(b) The angle of twist at the free end is found by using

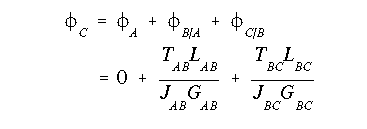
The torque T for each portion is found to be Tmax. The above equation for angle of twist is valid for homogeneous shafts. To be able to use this equation in portion AB, we need to know how much of the torque is carried by steel core and how much is carried by the aluminum shell. This, however, has been determined previously by examining the integral equation for torque in portion AB; that is, the first integral corresponds to the torque in the core while the second integral corresponds to the torque in the shell. These torques can also be obtained based on the fact that the angle of twist for the steel and aluminum is the same in portion AB.

The angle of twist at the free end is

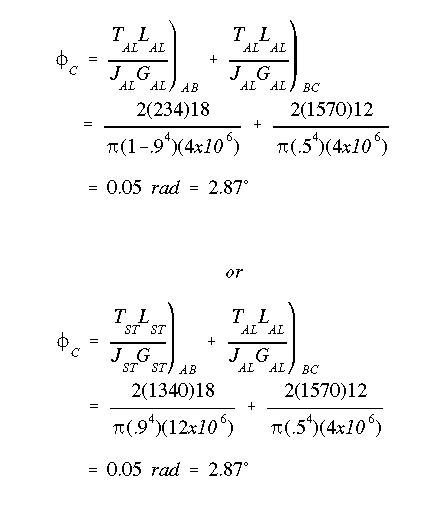
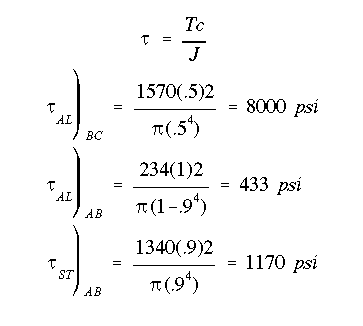
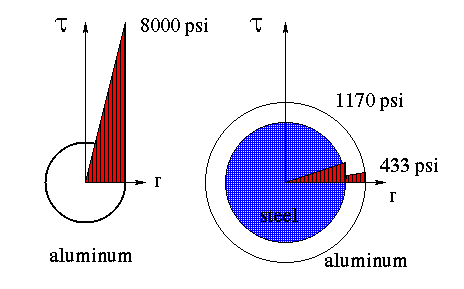
(c & d) To sketch the shear stress distribution in each section, the maximum shear stress must be found for each section. They are

To Section I.1

To Index Page of Pure Torsion