Direction Cosines of a Line: To define the orientation of a line in space, we need to know the angles that it forms with the axes of a given coordinate system. In most situations, these angles are difficult to measure, so we make use of analytic geometry and trigonometry to determine them.
Let's consider two arbitrary points P1 and P2. We use the Cartesian coordinates (x,y,z) to identify the position of each point. Then we consider a straight line passing through P1 and P2. The line segment between these two points has a length of d. To calculate the distance d between points P1 and P2, we use the following relationship
Based on the trignometric relationship between line segment d and its projection along each axis, we determine the direction cosines of the line as
where α, β, γ are the angles that the line makes with the positive x, y, z axes, respectively. A unique characteristic of the direction cosines is that they satisfy the condition
Therefore, if we know any two of the three angles, we can use Eq. (10) to find the third. |
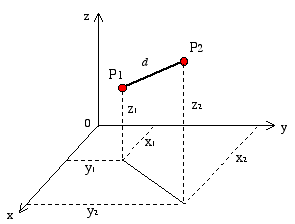
|
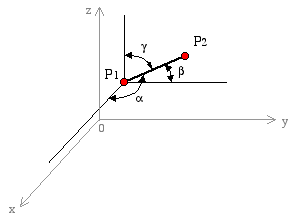
|
Animation of Cartesian Components and Direction Angles of a Vector
|
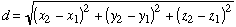 (8)
(8)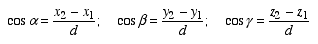 (9)
(9)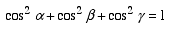 (10)
(10)