Example 8: A 200-kg sign is supported by the cable system shown below. Determine the tension developed in each cable to hold the sign in equilibrium.
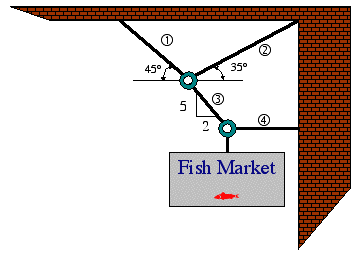
Solution
Step 1: A close examination of the cable system indicates that the two connection rings can be represented as two particles with the free-body diagrams shown below.
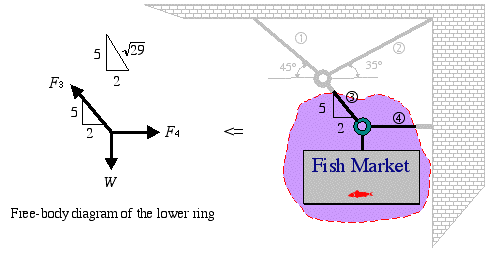
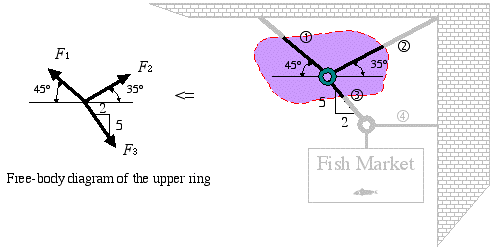
Each free-body diagram represents a coplanar force system.
Step 2: We continue by analyzing the free-body diagram of the lower ring next. This is because there are only two unknown forces in this case, and we can solve for them using the two equations of equilibrium.
Knowing the slope of cable 3 is 5/2, we find the hypotenuse of that triangle
as 
. Now, we can easily express
the horizontal and vertical components of F3 in terms of the slope and magnitude
of F3.
|
|
|
|
\With F3 known, the free-body diagram of the upper ring now has only two unknown forces, which are calculated similar to the previous case as follows
Solving the two equations simultaneously gives
Step 3, Analysis of Results: The results indicate that the tension in cable 3 is the highest among the four cables. With cable 4 being horizontal, the tension in cable 3 is 7.7% greater than the weight of the sign. This leads to the following question. What happens to the forces in cables 1, 2, and 3 if we were to eliminate cable 4? This scenario is examined next.
Design Modification and Analysis: By eliminating cable 4, the lower ring and the sign will move to the left and cable 3 becomes vertical. This change, however, has no impact on the position of the upper ring, and angles of cables 1 and 2 will stay the same as before.
Solution: The two free-body diagrams are shown below.
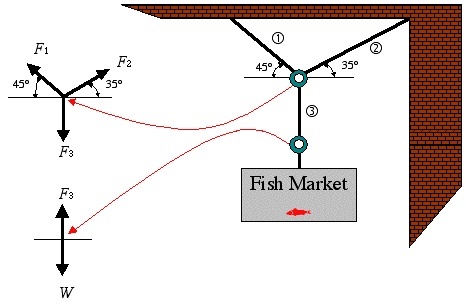
Since cable 3 is now vertical, it is easy to conclude that its magnitude, based on the equilibrium of forces in the vertical direction, is equal to the weight of the sign
|
|
Using the Free-body diagram of the upper ring, we obtain
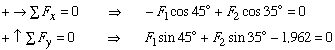
Solving the two equilibrium equations simultaneously gives
Therefore, by eliminating cable 4, we reduced the tensions in cables 3 and 1 by 7.2% and 22%, respectively, but increased the tension in cable 2 by 67.6%.