Example 3: Express the force vector in each case in its proper Cartesian vector form.

Solution:

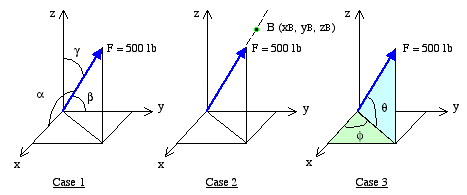
Case 1: 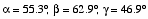. In this case, the coordinate direction angle between each axis and the force vector is specified. Thus, the force vector is found as

Case 2: x_B = 5 ft, y_B = 4 ft, z_B = 6 ft. In this case, the direction of the force vector should be determined based on the coordinates of two points along its line of action. We begin by expressing the force vector as the product of its magnitude and the unit vector along its direction

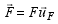
The unit vector in the direction of F is found from the position vector as

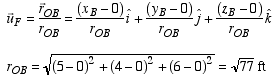
A simple multiplication gives the force vector in Cartesian form

Case 3: 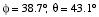. In this case, two projection angles of the force vector are specified. We begin by finding the z component of the force vector as

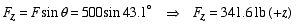
The projection of the force vector in xy plane is found as

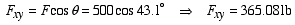
Now, by finding the projections of Fxy in x and y directions, we can find the x and y components of the force vector, respectively.