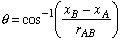Application of Unit Vector: In an alternative representation, the force of magnitude F is acting in the direction of line AB with coordinates of A and B clearly defined.
 |
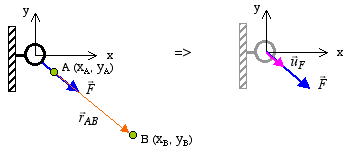In this case, we can represent 
in terms of its
magnitude and the unit vector in the same direction
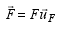
where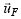 
is
the unit vector in the direction of . In this formulation,
the magnitude and the direction of the force vector are identified
separately whereas in the Cartesian formulation they are combined
together.
Position Vector: For calculation of the unit vector we make use of the position vector. We determine the position vector by subtracting the coordinates of its tail from those of its head as follows.
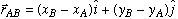
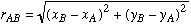
Knowing the position vector and its magnitude, we find the unit vector as
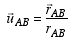
Notice that the angle q, used
previously to describe the direction of , can be determined
as
