Newton's Laws

First Law of Motion: A body originally at rest, or moving along a straight path with a constant velocity (zero acceleration), will stay in this state if no unbalanced force is acting on it. In this case, all the forces acting on the body are in balance or equilibrium. Mathematically, this statement can be expressed as

(1)

Second Law of Motion: If the body is subjected to an unbalanced force, it will accelerate in the direction of the unbalanced force. The acceleration rate is proportional to the magnitude of the unbalanced force. Mathematically, this law can be expressed as

(2)

where F is the unbalanced force and m is the mass of the body and 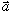its acceleration.

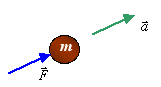
If a body is subjected to two or multiple forces, the acceleration will be in the direction of the resultant force. In that case, Eq. (2) can be rewritten as

(3)

If the forces acting on the body are in balance, then there is no resultant force (and no acceleration). In that case we arrive at the same equilibrium equation as defined by Eq. (1)

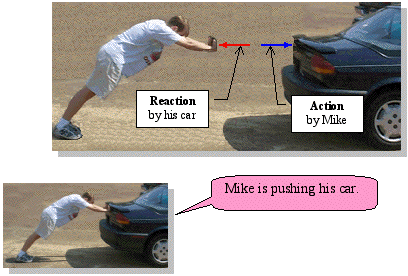
Third Law of Motion: For any action there is an equal, opposite and collinear reaction. The action and reaction forces are developed between two objects in contact, as depicted in the figure below. This law is extremely helpful in drawing free-body diagrams of particles and rigid bodies as will be discussed later.

Law of Gravitational Attraction: Newton describes the attraction force between two particles (e.g., earth and moon) as

(4)

where F is the magnitude of gravitation force, G is the universal constant of gravitation (66.73E-12 m ³ /(kg.s ² ) , M and m are the masses of the two particles, and r is the distance between the centers of the two particles. For an object on or near the earth's surface, the product GM/r ² is equal to the gravitational acceleration g, which has an average value of 9.81 m/s ² or 32.2 ft/s ² . Therefore, the earth's gravitational force on an object of mass m on or near its surface can be used to estimate the weight of the object according to the equation

(5)