Example 1: A person weighing 175 lb is standing on a 10-ft ladder weighing 25 lb, as shown in the figure. Determine the maximum height at which the ladder will be on the verge of slipping for

a. μ_A = μ_B = 0.3
b. μ_A = 0.3, μ_B = 0.15
c. μ_A = 0.15, μ_B = 0.3

Solution:

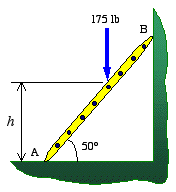
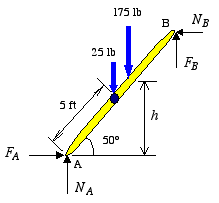
We begin by drawing the free-body diagram of the ladder and writing the equilibrium equations. Note that the friction force at each surface of contact is shown in opposite direction to that of impending motion. This is crucial as we will be using the friction equations along with those of equilibrium to solve the problem.

Equations of equilibrium:

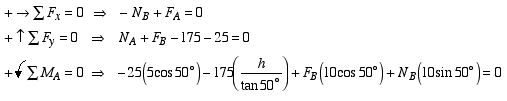
Friction equations:

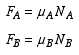
Substituting the friction equations into force equilibrium equations results in two equations and two unknowns (NA and NB). Notice that the magnitudes of the normal forces are independent of height h. Since we are interested in examining different values for coefficients of friction, it would be easier to write the three equilibrium equations in matrix form and solve for all three unknowns at one time.

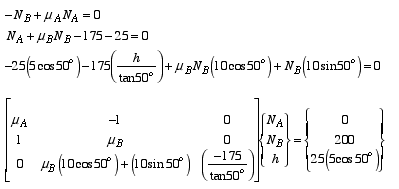
Part a: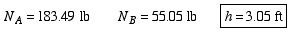

Part b: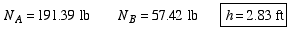

Part c: