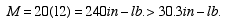
 |
 |
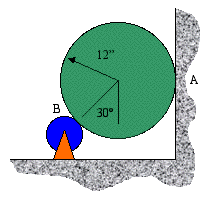
Example 3: A 20-lb wheel is supported by a free-rotating roller at B and the wall at A. Determine the moment required to initiate the rotation of the wheel in the clockwise direction. The coefficient of static friction at the wall is 0.25.
Solution:
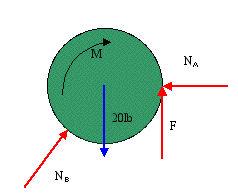
We begin by drawing the free-body diagram of the wheel. Since the roller at B is free to rotate, that means that there is no friction at the point of contact between the roller and the wheel. However, there is friction at the point of contact with the wall. If the wheel were to begin rotating in the clockwise direction, it would have to slide against the wall. Since the direction of motion is known, the friction force is shown in the opposite direction.
Next, we write the equilibrium equations as
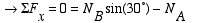 |
(1) |
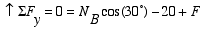 |
(2) |
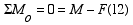 (3) (3) |
Since we have the condition of impending slipping at A, the friction force is related to the normal force at that point according to the friction equation
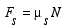 (4) (4) |
Substitute Eqn. 4 into Eqn. 2 for F, and solve Eqns. 1 and 2 simultaneously to get
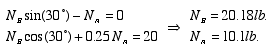
From Eqn. 3:
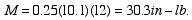
Is it possible for the wheel to roll up the wall before slipping?
For this motion to occur, there will be no contact between the roller and
the wheel at B, hence we set NB=0 in the equilibrium equation and
solve for the moment.