

Free-Body Diagram
 |
 Free-Body Diagram |
Example 2: The spool has a mass of 10 kg and rests against the wall and the floor having μ = 0.6. Determine the smallest value of P that causes an impending motion.
Solution:
We begin by drawing the free-body diagram of the spool, and identifying all the unknowns.
We must be careful with the direction of the friction force. So we consider the types of motion that can occur before deciding which way the friction force at A and B will be directed. In this case, the spool will either spin in the counterclockwise direction or possibly climb up the vertical wall because of the direction of force P. We draw the FBD based on the first scenario to begin the analysis.
The FBD shows a total of five unknown forces.Now, we proceed to write the three equilibrium equations as
 |
(1) |
 |
(2) |
 |
(3) |
| Note that we can use the moment equilibrium equation as we know the exact locations of the two normal forces. |
For the condition of impending slipping at A and B, the friction force at each point is related to the corresponding normal force according to the friction equations
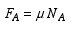 (4) (4) |
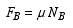 (5) (5) |
Now we have five equations to use to solve for the five unknowns. Substituting Eqns. 4 & 5 into Eqns. 1, 2 & 3 gives
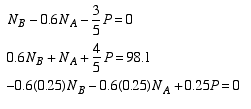
Writing these three linear algebraic equations in matrix form, we get
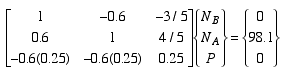
Solving the matrix equation for the three unknowns, we get
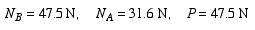
Therefore, a force of 47.5 N is necessary to have a condition of impending slipping at A and B.
We must also check to see if it is possible for the spool to climb up the vertical wall before it begins to slip. If we consider the instant at which such a motion occurs, we realize that the spool is no longer in contact with the floor at point A. Therefore, we set both normal and friction forces at A to zero. Now if we go back to Eqns. (1) through (3), we will have only three unknowns. Solving these equations for NB, FB, and P gives P = 54.5 N, which is greater than the value found previously. Thus, only slipping is a possible motion in this case.