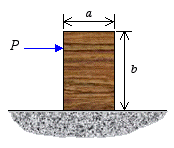
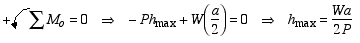Block on a Rigid Horizontal Surface
The maximum static friction force and kinetic friction force are
both related to the normal force at the surface of contact through
the relations
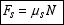 |
(1) |
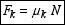 |
(2) |
where μs and
μk are the coefficients of static
and kinetic friction, respectively. In general, the values of
friction coefficients are dictated by the block and support surface
materials. Some typical values for
μs can be found in this Table.
The response of block to force P is captured in the following
four cases.
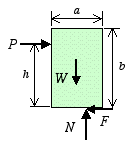
Case
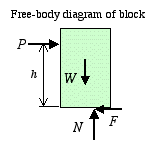
1: P < Fs, h < hmax. Block remains at rest and
the equilibrium equations indicate that
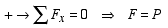
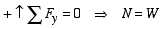
There is no relationship between the friction and the normal
force in this case.
|
 |
Case
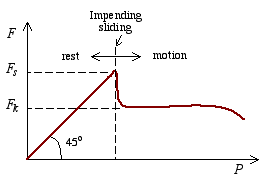
2: P = Fs, h < hmax. Block is about to slide
to the right. This impending motion is detected since P is now equal to the maximum friction force.
That is
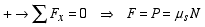
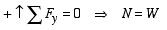
Case
3: P > Fs, h < hmax. Block will slide to the
right with an acceleration as the applied force is greater than the
maximum resistance or friction force at the surface of contact.
Once the block begins to slide, it is possible to maintain a
uniform (zero acceleration) motion by reducing the value of P to that equal to the kinetic friction 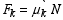 .
.
Case
4: Combination of P and h causing the block to tip over. In this case,
the position of the normal force is clearly defined to be at the
right edge of the block as that is the only place where the block
is in contact with the horizontal surface. To determine whether
tipping is a possibility or not, we solve for the value of hmax using the moment equilibrium
as
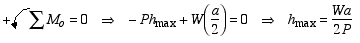
If h = hmax and P < Fs, then the block is on the verge
of tipping over with no possibility of sliding.
If b  h
h 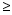 hmax and P < Fs, then the block will tip over
with the right edge remaining stationary relative to the horizontal
surface.
hmax and P < Fs, then the block will tip over
with the right edge remaining stationary relative to the horizontal
surface.
If h = hmax and P = Fs,
then both tipping and sliding are impending. There is an equal
chance that the block will either tip over or begin to slide.
Example 1
Example 2
Example 3
Example 4
Example 5
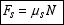
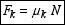
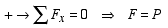
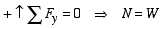

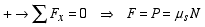
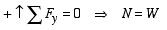
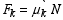 .
.