Text TBD
Proportional Limit: Also known as the elastic limit, is the point where the stress-strain curve becomes nonlinear. The stress and strain values at this point are known as the proportional-limit stress and strain, respectively. This is the point beyond which Hooke's law can no longer be used to relate stress and strain in axial or shear deformation. The figure below shows the proportional limit point associated with axial loading. A similar point also exists in shear stress-strain curves. |
 |
 |
The yield point corresponds to the point where the material begins to have permanent (unrecoverable) deformation. While some materials have a well-defined yield region (Figure A), others (Figure B) do not. In the absence of a distinct yield point, a 0.2% offset is used to obtain an approximate yield point. Although the yield and the proportional limit points are close to each other, they do not correspond to the same location on the stress-strain curve. The stress and strain corresponding to the yield point are called the yield stress and yield strain, respectively. |
 |
0.2% Offset:
The 0.2% offset point is determined by drawing a line parallel to the linear region of the curve starting from point 0.002 on the strain axis. The intersect of this line and the stress-strain curve defines the 0.2% yield point.
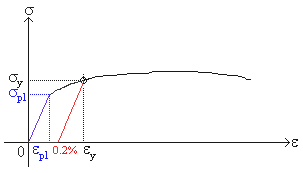
Ultimate Tensile Strength:
The maximum tensile stress a material is capable of carrying is known as the ultimate tensile stress. It corresponds to the highest point on the tensile stress-strain curve. The tensile ultimate stress is usually denoted by stu. The corresponding strain is known as the ultimate tensile strain.
A crucial point to remember is that the ultimate tensile stress is usually based on the original cross-sectional area of the specimen. As such, its value on an Engineering stress-strain diagram would be different from that on the True stress-strain diagram if the specimen demonstrates considerable necking prior to fracture. It is a common practice to use the value associated with the engineering stress-strain diagram.
Ultimate Compressive Strength:
The maximum compressive stress a material specimen is capable of carrying is known as the ultimate compressive stress. Unlike in the case of tension, the compressive response of a specimen is a function of its cross-sectional shapeand length. To eliminate these geometric effects, compressive specimens are usually designed to be very short with a relatively large cross-sectional area. If the material is brittle, like concrete, then failure at the ultimate point is the form of fracture. If the material is ductile, like aluminum, then failure is in the form of excessive yielding, and as such, there is no definite value for the ultimate compressive stress of a ductile material. In the case of ductile materials it is common to assume scu= stu.
Modulus of Resilience: It refers to the capacity of a material to absorb energy in the elastic range. Its value is simply equal to the area under the elastic region of the stress-strain curve. For any linearly elastic material, the modulus of resilience is found as U = 0.5seee or U = 0.5se2/E where se is the elastic-limit or proportional-limit stress of the material. |
 |
 |
 |
Refers to the capacity of a material of absorb energy prior to failure. Its value is equal to the entire area under the stress-strain curve. In most cases, the area under the elastic portion of the curve is a very small percentage of the total area and may be ignored in the calculation of the modulus of toughness. To further simplify the calculation, the nonlinear portion of the stress-strain curve is approximated by a series of straight lines as shown to the left. In the example to the left, the modulus of toughness is determined by summing the areas A1 through A4. |
Young's Modulus: Also known as the Modulus of Elasticity, is a measure of material resistance to axial deformation. Its value is obtained by measuring the slope of the axial stress-strain curve in the elastic region. It is named after the English scientist Thomas Young. It is usually denoted by E,and has units of N/m2 or lb/in2. Since in some materials Young's modulus in tension is different from that in compression, subscript c or t is used to simplify the distinction. Test Your Knowledge! |
 |
 |
Tangent modulus is defined as the slope of a line tangent to the stress-strain curve at a point of interest. Tangent modulus can have different values depending on the point at which it is determined. For example, tangent modulus is equal to the Young's Modulus when the point of tangency falls within the linear range of the stress-strain curve. Outside the linear elastic region, at point A shown for example, tangent modulus is always less than the Young's modulus. Tangent modulus is mostly used to describe the stiffness of a material in the plastic range, and it is denoted by Et. Ramberg-Osgood Equation: It is used to describe the stress-strain relationship in the yield region of the stress-strain diagram. It uses three different properties of a material, i.e., E - Young's modulus, s0.7 - stress value corresponding to the secant modulus of 0.7E, and n- shape factor describing the shape of the stress-strain diagram in the yield region.
|
The Ramberg-Osgood equation is used in inelastic buckling analysis of columns and plates.
Secant Modulus: Secant modulus is the slope of a line drawn from the origin of the stress-strain diagram and intersecting the curve at the point of interest. Therefore, the secant modulus can take different values depending on the location of intersect. The figure below shows how the secant modulus is obtaind at point A on the curve. The secant modulus can be expressed as a percentage of the Young's Modulus (e.g., 0.7E or 0.85E), and it is used to describe the stiffness of a material in the inelastic region of the stress-strain diagram. Secant modulus is commonly denoted by Es. |
 |
Poisson's Ratio: The ratio of the lateral strain to axial strain is referred to as the Poisson's ratio of a material. The calculation is based on the physical phenomenon described in the figure below.
Test Your Knowledge!
Shear Rigidity: Also known as Modulus of Rigidity, is a measure of material resistance against shear distorsion. Its value is equal to the slope of the shear stress-strain curve in the elastic region. It is usually denoted by G, and has units of N/m2 or lb/in2.
Ductility: The capacity of a material to undergo large inelastic deformation prior to fracture. It is highly dependent on the operating temperature of the material. At very low temperatures materials tend to lose their ductility and become brittle.
Elongation:
A measure of material ductility, it is defined as the percent change in the specimen length at the point of fracture. Usually denoted by e, it can be obtained by multiplying the fracture strain by 100.
e= (L'-Lo/Lo)100
Where L' = specimen gage length after fracture, Lo= original gage length. Note that since percent elongation is determined as a function of gage length, it is important to specify the gage length when mentioning percent elongation.
