Equivalent Systems

If a force acting on a body is represented (or replaced) by another force or a force-moment system (at a different point on the body) such that the resulting rigid-body effects (i.e., translation and rotation) remain unchanged, the two systems are said to be statically equivalent. We are interested in this concept because in many statics problems, it may be more convenient to replace the existing force with another equivalent force or force-moment system.

Notice that although it is possible to keep the rigid-body effects the same, it is impossible to keep the internal effects such as stresses the same when we move the force from one location to another. So the idea of equivalent systems is only to help with the statics of a rigid body. We examine the topic of equivalent systems by looking at three different cases as described below.

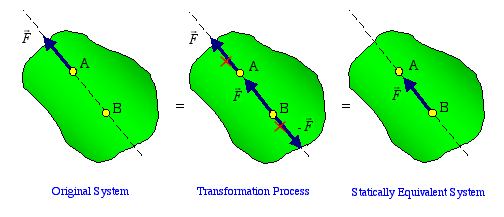
Case 1: Equivalent Force at an Arbitrary Point Along the Same Line of Action: Let's represent (replace) the force acting at point A by a statically equivalent system at point B. In this case, point B is along the line of action of the force at A. The statically equivalent system is found by adding two equal and opposite forces at point B such that each has the same magnitude as the original force and is parallel to it as shown below. Since the two equal and opposite forces shown at point B cancel each other, there is no net change to the loading system in the transformation process. Canceling the force Fat A with -Fat B gives the statically equivalent force at B.

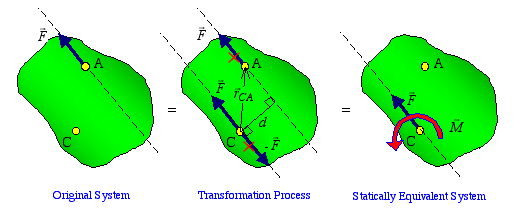
Case 2: Equivalent Force at an Arbitrary Point Away from its Line of Action: Let's represent (replace) the force acting at point A by a statically equivalent system at point C. In this case, point C is not along the line of action of the force at A. The statically equivalent system is found by adding two equal and opposite forces at point C such that each has the same magnitude as the original force and is parallel to it as shown below. Although the force Fat A added to -F at B results in a zero net force, there remains a couple of magnitude M = Fd,which gives rise to a statically equivalent force-couple system at C. Hence, when the force is moved to a point away from its line of action, it will be accompanied by a couple moment.

In vector form, the couple moment is found as

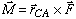
Since the magnitude of the couple moment is only a function of the force magnitude and the perpendicular distance between the force couple, it can be applied at any point on the body without changing its effect. This is also the reason no subscript is shown on the couple moment in this case.

Resultant of Coplanar Forces: In calculating the force resultant, both force and moment equivalency must be satisfied. In other words, the sum of moments produced by individual forces about a point must be equal to the moment produced by the resultant force.

A special case of a coplanar force system is that of parallel forces commonly encountered in lateral loading of beams. What we know about such systems is that the direction of the resultant force is parallel to those of individual forces, but we may not know its sense and location. This topic is explored further in the following examples.

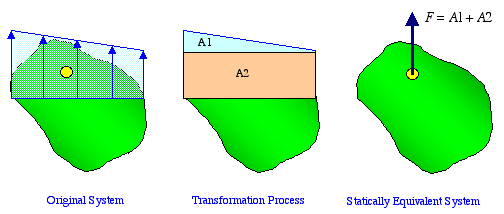
Case 3: Distributed Force Replaced by an Equivalent Concentrated Force: In this case, a distributed force is replaced by its resultant acting at the centroid of the distributed area. The magnitude of the resultant force is simply equal to the area of distribution. It is necessary for the resultant force to be in the same direction as the distributed force as shown below.

Key Observations:

We can slide a force to anywhere along its line of action without changing its rigid-body effect. On the other hand, if we move the force to a point away from its line of action, then we must also include the accompanying moment. In either case, we cannot change the magnitude or direction of the force.