Moment about an Axis: Consider the
force 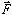 passing
through point A as shown in the figure.
passing
through point A as shown in the figure.
The view from the y axis reveals that 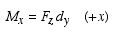
where 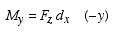 |
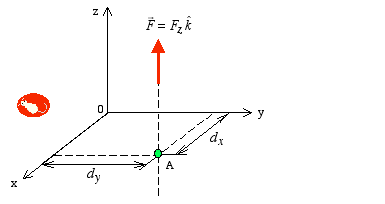
|
where 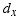 is the moment
arm of the force with respect to the y axis. In this case, the
moment axis is pointing in the negative y direction. Also as to be
expected, is the moment
arm of the force with respect to the y axis. In this case, the
moment axis is pointing in the negative y direction. Also as to be
expected, 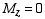 since since 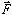 is parallel to the z
axis. is parallel to the z
axis.
|
We can now expand this discussion to the case of calculating the moment about an arbitrary line aa. Two commonly encountered cases are described next.
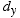 is the moment
arm of the force with respect to the x axis. In this case, the
moment axis is pointing in the positive x direction as shown.
Similarly, the
is the moment
arm of the force with respect to the x axis. In this case, the
moment axis is pointing in the positive x direction as shown.
Similarly, the 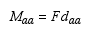 (6)
(6)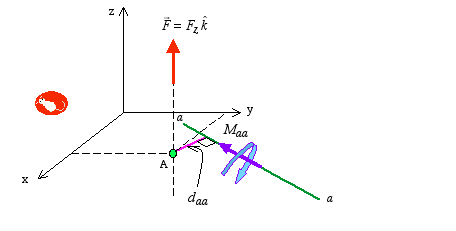
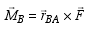
 along line
along line 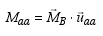 (Magnitude of the component)
(Magnitude of the component)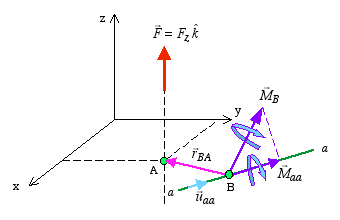
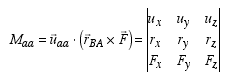 (7)
(7)
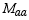 comes out negative, it simply means that its direction is opposite
to that defined by
comes out negative, it simply means that its direction is opposite
to that defined by 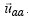 This projection can also be put in vector form as
This projection can also be put in vector form as
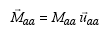 (8)
(8)