Principle of Moments: Depending upon the direction of the force vector, it may be difficult to directly measure the moment arm das in Eq. (1). In those situations, we break the force into its individual components, and find the moment as the sum of the moments of individual components as
 |
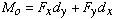(3) |
Care should be taken to account for the direction of each moment component in Eq. (3). This approach is generally referred to as the Principle of Moments,which simply indicates that the moment of a force is equal to the sum of moments of its components.
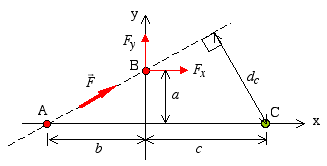
Consider force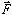 
acting along
the line passing through points A and B. To find the moment of this
force about point C, we need to know its moment arm designated as
dc. If this distance is not readily available, then it
is easier to apply the principle of moments. Since force is a
sliding vector, it can be placed at any point along its line of
action. Let's slide it up to point B, and break it into its x,y
components. The moment about point C is found as
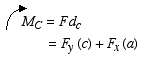
Notice that both moments are in the clockwise direction. Once we know the moment about C, we can solve for the moment arm (if it was of interest) as
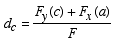
Five-Minute Exercise: Prove that the moment about point C will stay the same if the force is moved to point A instead of B. Let F= 200 lb, a= 3 ft, b= 4 ft, and c= 6 ft.