Scalar Representation: Consider force
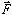acting at point A. The magnitude
of the moment of this force about point B is determined from the
scalar product
 |
(1) |
where F is the magnitude of the force, and d is the perpendicular distance between point B and the line of action of the force. Distance d is commonly referred to as the moment arm of the force while point B is called the moment center.
In this case, the moment about point B can be interpreted as the
measure of the tendency of force F to cause the body to rotate
about B. The key word is tendency. It is not necessary for the body
to actually rotate about B for the moment to be created. The sense
of the moment is determined based on the right-hand rule. The axis
of the moment vector is perpendicular to the plane containing 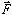and d.
To calculate the moment of a force using the scalar approach, we must know:
Force magnitude
Location of the moment center
Perpendicular distance from the moment center to the line of action of the force