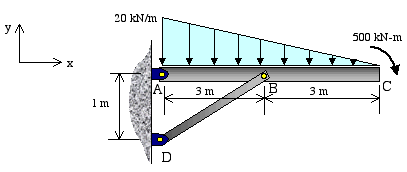
Example 1: The purpose of this example is to demonstrate the drawing of a free-body diagram in a step-by-step fashion. The focus is on beam ABC.

Step 1: Separate beam ABC from the rest of the system and represent it by a simple sketch.

Step 2: Show the couple moment as is, but replace the distributed force by its equivalent resultant. Don't calculate the magnitude of the resultant force at this time. Simply show it as a single force passing through the centroid of the distribution in the direction consistent with that of the distributed force.

Step 3: We have a pin support at point A. So, the reaction force must be represented by two components in x and y directions. We label them as RAx and RAy, respectively, and show each in an assumed sense. The correct sense for each reaction will be determined once we formulate the equilibrium equations, and solve them for the magnitude of reactions.

At point B, the beam is connected to member BD by a pin. The small circle drawn at point B indicates a pin joint. Since rotational movement is not restricted at this joint, there is only a contact force between the two members and no moment. Furthermore, a careful examination of member BD indicates that it is a two-force member; therefore, the contact force must be directed along line BD. We assume a sense for the force at B and show that on the free-body diagram.

Finally, we calculate the resultant of distribution. Since the distributed force is triangular, the resultant force is found as

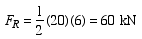
The complete free-body diagram of beam ABC is shown below.

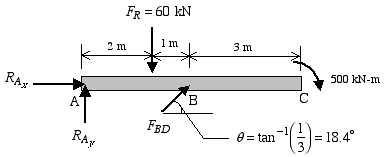
With the help of the FBD, we can identify all the unknown loads that need to be determined. In this case, there are three unknown forces. We can find their magnitudes using the equilibrium equations.