Solution: We begin our analysis by first drawing the free-body diagram of the beam. Once we have the unknown reaction loads identified, we solve for them using the equilibrium equations.

Free-Body Diagram of Beam: The beam is supported by a pin at point A and a horizontal roller at point D. Therefore, there are two unknown reactions at point A and one at point D as shown below. Notice that in drawing the free-body diagram we assume a direction for each reaction load. The correctness or incorrectness of each assumed direction will be determined by solving for the magnitude of each reaction load. Also to simplify the calculations, the distributed force is represented by its resultant acting at its centroid.

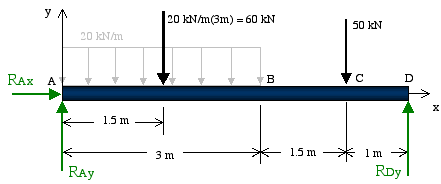
Reaction loads: As shown in the free-body diagram, there are three unknown reactions that need to be solved for using the equilibrium condition. Since this represents a two-dimensional force system, we can only make use of three equilibrium equations. Various options were explained previously, and here we demonstrate the solution with only one option.

We begin the solution by using the equilibrium of moments with point A as the moment center. We choose point A as it contains two out of three unknown reactions.

Positive sign on the reaction indicates its assumed direction is correct. Now we proceed with solving the remaining two reaction forces. Using the equilibrium of forces in the x direction gives

=>

The horizontal reaction force at A is zero as there is no other horizontal force acting on the beam.

=>

Verification of Results: We can do a simple check to verify the answers. Since the external forces are all in the vertical direction, the sum of external forces must be equal in magnitude with the sum of reactions in the vertical direction. This is shown below

We can also verify the solution by summing moments about D or any other point to see if it is equal to zero.

=>

=>

If there is no error in the analysis, the value of e should be zero, or very close to zero, as is the case here, considering truncation and/or round off error. Therefore, we are confident that our answers are correct.