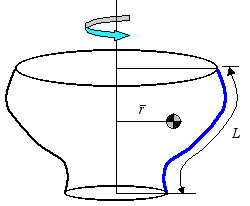
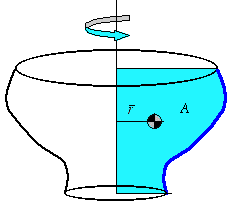
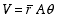If a curve is revolved about a nonintersecting axis, the area of the resulting surface of revolution is equal to the length of the revolving curve times the distance traveled by the centroid of the curve.
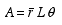 |
(1) |
where Ais the surface of revolution,
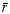 is the perpendicular distance
from the centroid of the curve to the axis of revolution
θ is the angle of revolution measured in
radians, and Lis the length of the
revolving curve.
is the perpendicular distance
from the centroid of the curve to the axis of revolution
θ is the angle of revolution measured in
radians, and Lis the length of the
revolving curve.