Example 2: Calculate the moment of inertia of the shaded area about the x axis.
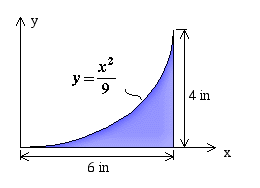
Example 2: Calculate the moment of inertia of the shaded area about the x axis.

Solution: The solution is presented based on three different choices of differential area to show the variation in the solution process.
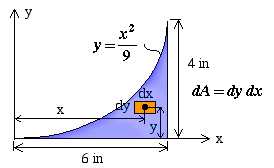
Case 1: Choose a small rectangle of dimensions dx, dy as the differential element.
For this choice of differential area, the moment of inertia about the x axis can be found by using the equation
where y is the moment arm of differential area dA with respect to the x axis. Replacing dA by dy dx changes the equation into a double integral with the specified limits |
 |
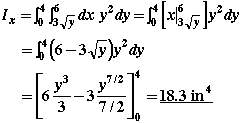
Case 2: Choose a horizontal rectangular strip for the differential area as shown below.
Note: Since all parts of dA are at the same y distance from the x axis, we can still use the same equation as in Case 1
where y is the moment arm of the differential area dA with respect to the x axis. Notice that in this case the differential area has a width of 6 - x and a height of dy. In this case, we will have a single integral along the y axis with limits of 0 and 4 expressed as | 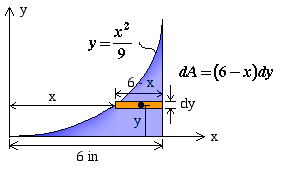 |
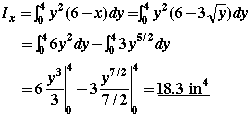
Notice that the limits of integration is set by the differential length dy. If we were to write the integral in terms of x, we would have to take the following steps to get rid of all variables involving y in the equation
Knowing 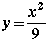 , then
, then 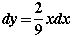 and
and 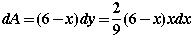 .
.
Also at x = 0, y = 0 and at x = 4, y = 6. With these substitutions, the integral equation becomes
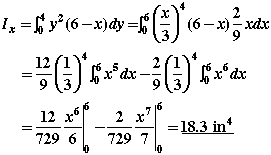
The answer is the same as that found previously.
Case 3: Choose a vertical rectangular strip for the differential area as shown below.
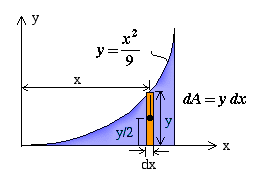
In this case, all parts of dA are not at the same y distance from the x axis. Therefore, we cannot use the formula used in Cases 1 and 2 to find Ix. Instead, we must use
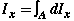
We need to first determine the moment of inertia of the differential element with respect to the x axis, then integrate it over the entire area to find Ix.
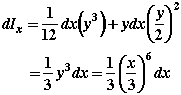
Having found the moment of inertia of dA about the x axis, we then integrate it to find Ix.
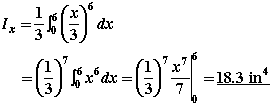
Notice that the limits of integration are set by the differential dx.