Principal Axes and Principal Moments of
Inertia: 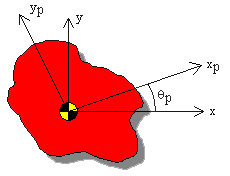 The principal axes are those for which
the product of inertia is zero. For any arbitrary shape there
exists a set of axes which result in zero product of inertia. The
orientation of principal axes with respect to the centroidal
coordinates x and y can be obtained using
The principal axes are those for which
the product of inertia is zero. For any arbitrary shape there
exists a set of axes which result in zero product of inertia. The
orientation of principal axes with respect to the centroidal
coordinates x and y can be obtained using
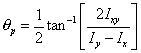 |
(10) |
where Ix, Iy, and Ixy represent the moments of inertia about the x-axis, moment of inertia about the y-axis, and the product of inertia with respect to x and y axes, respectively. The angle θp is measured positive counter clockwise from the centroidal x-axis.
Based on the above definition, if either x or y is an axis of symmetry, then they both are considered as principal axes as Ixy and hence θp would be zero in that case.
The moments of inertia about the principal axes are expressed as
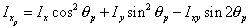 (11) (11) |
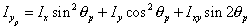 (12) (12) |
Key Observations:
A key factor to remember is that the sum of moments of inertia about any two perpendicular axes in the plane of the area is constant. This implies the following:
![]()
Another important fact to remember is that between Ixp and Iyp one represents the minimum while the other represents the maximum moment of inertia for the shape considered. This fact is crucial in design of beams for minimum deflection. If the load on a beam is applied perpendicular to the cross-sectional axis with the largest moment of inertia, then the resulting deflection is the minimum for that shape and size beam.