and 
measured from the specified reference axes. Example 1:
For the surface geometry shown, calculate the coordinates of the centroid and measured from the specified reference axes.
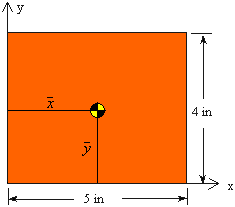
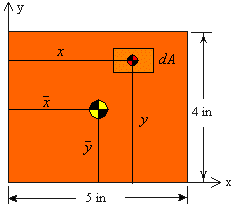
Solution: Although the shape shown is a simple rectangle, it would be useful to see how we would calculate its centroid using the integral equations. We solve this problem based on two different choices for the differential area.
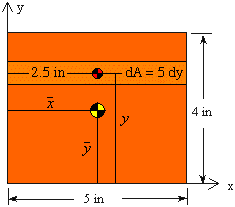
In the first case, a rectangular area of height dy and width of 5 in. is used as the differential area. The solution involves single integrals as demonstrated below. Notice that the centroid of the differential area is defined by the coordinates (2.5, y) in this case.
 |
 |
 |
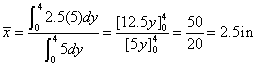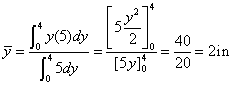An alternative solution involves using a differential area of height dy and width dx. In this case, we see double integrals in both numerator and denominator of each equation. Also note that the centroid of the differential area is at (x, y).
  |
|
 |
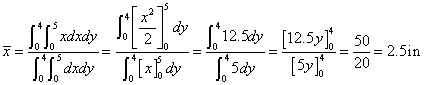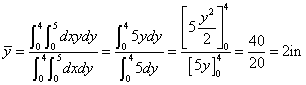