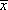 and
and
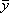 ) of the shaded area with respect to
the reference axes.
) of the shaded area with respect to
the reference axes. Example 2:
Locate the centroid (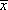 and
and
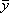 ) of the shaded area with respect to
the reference axes.
) of the shaded area with respect to
the reference axes.
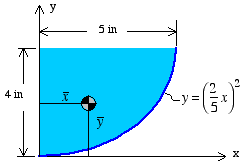
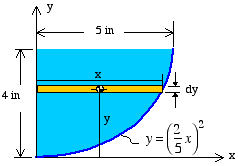
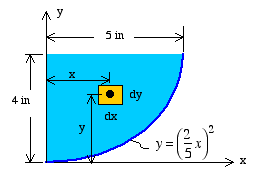
Solution: To solve for the centroid location, we must first choose an appropriate differential area. In this example, we choose a horizontal rectangle of width xand height dy.
Differential area: dA = x dyThe x coordinate of the centroid is found as
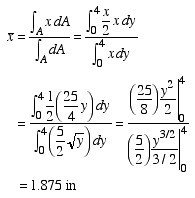 |
|
To find the y coordinate of the centroid, we use the same differential element and write
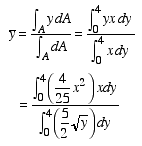
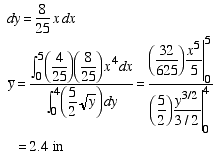
Therefore, the centroid of the shaded area is at
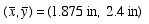
Alternate Solution: Let's consider the solution with a different choice of differential element.
Differential area: dA = dx dy
Because of the choice of differential area, the integral over the area changes into a double integral over x and y. In this case, the selection of limits must consider the boundaries in x and y directions.

| 
|
The solution for the y coordinate of centroid can be obtained in a similar fashion.