and 
measured from the specified reference axes. Example 3:
For the composite shape shown, calculate the coordinates of the centroid and measured from the specified reference axes.
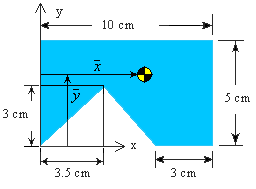
Solution:
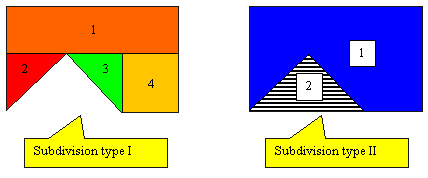
Since the boundary consists of a series of straight lines, we can subdivide this composite shape into a collection of simple elements with well-defined centroids of their own. In this case there are two ways of calculating the centroidal coordinates and . Subdivision type I divides the shape into four elements, two rectangles and two triangles.
On the other hand subdivision type II takes a simpler approach of considering a 5x10 rectangle and the missing area which is a 3x7 triangle. Either approach will provide the correct answer, but type II will obviously take a lot less time.
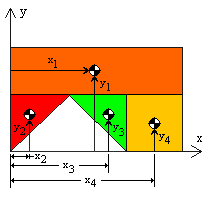
For subdivision type I the centroidal coordinates are found as
 |
|
 |
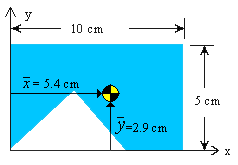
where x1, x2, x3, x4, y1, y2, y3, and y4 correspond to the centroidal coordinates of the four elements, respectively, measured from the reference y and x axes as shown. For the specified dimensions the centroid is found to be at
 |
= 5.4 cm |
 |
= 2.9 cm |
Notice that because of the choice of reference coordinate system all x and y values of individual elements are positive. Depending on the choice of reference axes, it is possible for these terms to be negative. Thus, one must be careful with the signs of x and y in calculating the centroid of a composite shape. Think of x and y as algebraic distances, not as lengths.
The alternative approach with subdivision type II results in simpler equations for and as demonstrated below.
|
|
 |
| where A1 represents the area of the 5x10 rectangle and A2 represents the area of the cutout triangular section. |
 |
= 5.4 cm |
 |
= 2.9 cm |
It is always a good idea to examine the results to make sure they make sense. We know that the centroid of the 5x10 rectangle without any cutout would be at 5 cm to the right of y-axis and 2.5 cm above the x-axis. With the cutout being in the lower left region of the rectangle, we would expect the centroid to shift in the upper right direction. The solution results indicate the shift in the expected direction.