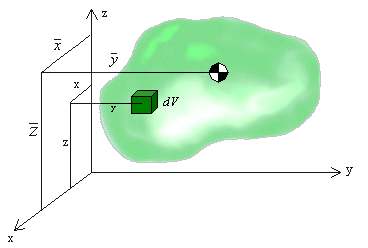
Centroid of Volume: The equations for calculating the centroidal coordinates of a volume of arbitrary shape are given as
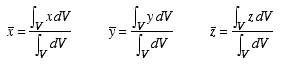 |
(1) |
Each integral is evaluated over the entire volume. The x, y, and z terms inside the integrals denote the distances measured from the reference axes to the centroid of the differential volume. Depending on the choice of differential volume dV, a single, double, or a triple integral formulation may be used. For some problems it may be possible to choose a differential volume that has a fixed cross-sectional area and a variable depth. This leads to a one-dimensional integral in both the numerator and the denominator.
As was demonstrated in earlier sections, if a three-dimensional body can be represented in terms of simple geometric elements, then the integrals can be replaced by simple sums as
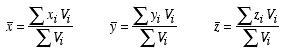 |
(2) |
where xi, yi, and zi represent the centroidal coordinates of each element with respect to the reference coordinate axes. Thus, each can be either positive or negative.
The procedure for calculating the center of volume is described in the following example.
Center of Mass: Since mass and volume of a body are related through a constant of proportionality (i.e., the density), it is possible to calculate the center of massas
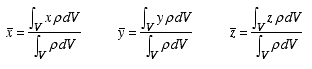 |
(3) |
In this case the differential mass dmis represented by rdV. Of course, if the body is homogeneous (r= constant), then there is no difference between the center of volume and center of mass.
If a body can be represented in terms of multiple discrete elements with different densities, then the center of mass can be found using
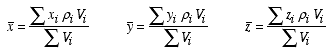 |
(4) |