The point corresponding to the geometric center of an object is known as the centroid. Depending on the shape of the object, one, two, or three coordinates may be needed in order to define its exact position in space. If a shape possesses an axis of symmetry, then its centroid will always be located on that axis. If it has two or multiple axes of symmetry, then its centroid will coincide with the intersection of those axes. The two shapes shown below demonstrate this fact. |
|
 It is possible for the centroid of an object to be located outside of its geometric boundaries. For example, the centroid of the curved section shown is located at some distance below it.
It is possible for the centroid of an object to be located outside of its geometric boundaries. For example, the centroid of the curved section shown is located at some distance below it.
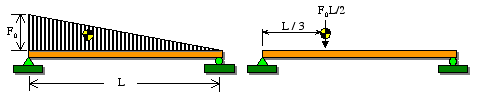
The centroid of a distributed load is also an important consideration in the context of statics and mechanics of materials. For example, if the distributed load shown below is replaced by its resultant acting at the distribution centroid, the resulting support reactions remain the same.