Zero-Force Members: Occasionally we encounter truss members that carry no force. There are two conditions that can cause a member to become a so-called zero-force member.
Condition 1:
|
1.1 Two non-collinear members are connected at a joint. 1.2 No applied force or support reaction present at that joint. 1.3 Both members are zero-force members. Note that the truss members are assumed to have negligible weights. Let us examine the truss shown below to look for zero-force members. We begin by identifying the so-called candidate joints where we have no external force or reaction. |
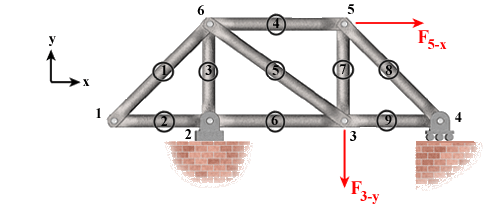 |
Candidate Joints: By looking at all the six joints, we identify joints 1 and 6 as candidate joints.
Of these two joints, joint 6 is eliminated from consideration because there are four members connected together at that joint. However, at joint 1 there are only two non-collinear members. Therefore, we conclude that members 1 and 2 are zero-force members in this case. This means that as long as the support and loading conditions remain as shown, members 1 and 2 and subsequently joint 1 can be eliminated without changing the internal load distribution of the truss.
Is it possible to have a force at the joint where two members are joined together, and have one of the members be a zero-force member?
The answer is yes. If the force or support reaction is collinear with one of the two members, then the non-collinear member will be a zero-force member. This is demonstrated in the figure. The external force at joint 1 is directed along member 2, therefore, member 1 is a zero-force member in this case.
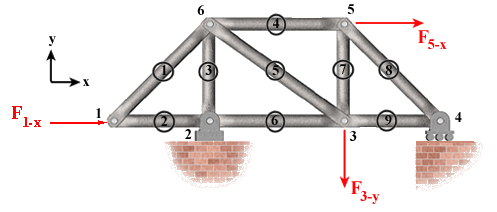
Condition 2:
|
2.1 Three members are connected together at a joint. 2.2 Two of the members are collinear. 2.3 No external force or support reaction is acting at that joint in the direction of the non-collinear member. 2.4 The non-collinear member is a zero-force member. |
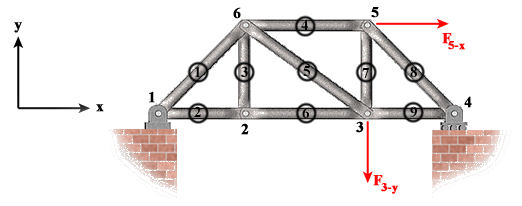
|
Let us make one change to the truss examined before, and then look for members that meet the condition stated here. We move the support from joint 2 to joint 1 as shown below.
Once again we identify the candidate joints. In this case, joints 2 and 6 are candidate joints as no external force or support reaction is present at those joints. Joint 6 is eliminated from consideration as there are more than three members connected together at that joint. Joint 2, on the other hand, meets the specified condition. Members 2 and 6 are collinear, member 3 is the non-collinear and hence the zero-force member in this case.
So we could remove member 3 from the truss. But, we have to be careful about something else. Notice that by removing member 3, even though it is a zero-force member, joint 2 is no longer stationary. This makes the truss unstable. Therefore, we must eliminate joint 2 entirely. We can do this by removing members 2 and 6 and replacing them by a single member connecting joints 1 to 3. In that case, we would end up with another stable truss.
Another consideration is this. Is it possible for more zero-force members to be revealed as a result of identifying and removing the known zero-force members. The answer is yes it is possible.
Let us examine the truss to see if this condition occurs in this case. We identified member 3 as being a zero-force member that could be removed. Now if we reconsider joint 6, we see that there would only be three members connected at that joint. Is it possible that one of these members is a zero-force member?
The answer in this case is NO. Notice that the condition stated that of the three members coming together at a joint, two had to be collinear. That condition cannot be satisfied at joint 6 even with member 3 removed. So member 3 is the only zero-force member in this case.