Support Requirements


The purpose of using supports is to prevent the truss from moving under the application of external forces. If the supports adequately restrain the truss against translation and rotation, we have a proper support system; If the supports do not provide adequate restraining, we have an improper support system. If the support conditions are proper, the equations of static equilibrium will be satisfied. For a two-dimensional (planar) truss under a two-dimensional loading system (in the plane of the truss), the scalar equilibrium equations expressed as

ΣFx = 0 (1) (equilibrium equation for forces in the x direction)
ΣFy = 0 (2) (equilibrium equation for forces in the y direction)
ΣMo = 0 (3) (equilibrium equation for moments about an arbitrary moment center "o")

may be used to validate the adequacy of the supports.

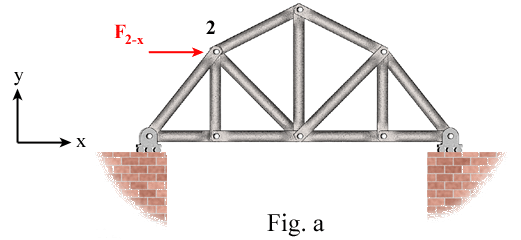
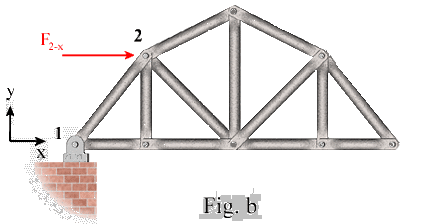
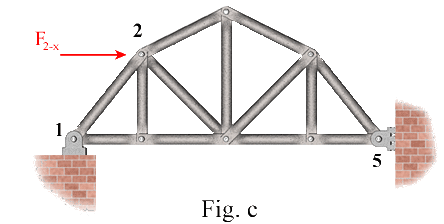
Improper Supports: Equilibrium is violated under two conditions:

For example, the truss shown in Fig. a is not adequately restrained against translation in the x direction. Therefore, as the external force F2-x is applied, no horizontal reaction is created at either of the two supports to satisfy the equilibrium of forces in the x direction.

mouseover figure

The trusses, shown in Figs. b and c, are not adequately restrained against rotation about the pin support at joint 1. Therefore, the moment equilibrium would be violated as a result of the applied force F2-x. This violation becomes evident by summing moments about joint 1. For the truss in Fig. b, the moment created by F2-x is not balanced by any other moment. For the truss in Fig. c, the horizontal reaction force at joint 5 has no moment arm about joint 1, therefore, it would not appear in the moment equilibrium equation.

mouseover figure

mouseover figure

Redundant Supports: Unlike the previous condition, in this case the truss is over-restrained. This condition is developed when there are redundant supports. For example, if a truss is supported by a hinge or pin support at two different locations, then we will have redundancy in support reactions. This situation is examined in the next section.