Solution: We begin the solution by drawing the free-body diagram of the system as a whole. This diagram reveals the presence of four unknown reactions at joints A and D. Clearly, we cannot solve for them using this free-body diagram as we could only apply three equilibrium equations to it.

What we should do is to break up the frame structure into individual components represented by separate free-body diagrams as shown below.

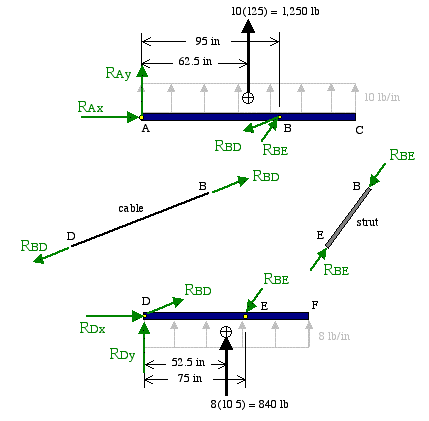
Members BD and BE are recognized as being two-force members as each is loaded only at two points. As a result we know the direction of axial force in each case although their respective magnitudes are unknown. This understanding provides the gate to the solution in this case.

Next, if we examine the free-body diagrams of beams ABC and DEF, we find that they both have reactions RBD and RBE in common. Since we can write three equations of equilibrium for each beam (represented by a two-dimensional non-concurrent force system), we can have up to six unknown forces, and that is exactly what we have here. We know the directions of all the unknown forces but not their magnitudes.

However, we cannot solve for all the unknown forces acting on one beam and then determine those acting on the other because each has four unknown forces. What we need to do is to determine the force RBE using the equilibrium of beam DEF first, then solve for force RBD using the equilibrium of beam ABC. Having done that, we would then be left with only two unknown forces in each case.

We begin the solution by first finding the slope of cable BD and that of strut BE using the triangles shown below. These triangles help in writing the x,y components of the two axial forces.

Using the equilibrium of moments in beam DEF with the moment center at point D gives

=>

=>

Positive sign confirming the assumed direction is correct. Now by using the equilibrium of moments in beam ABC with the moment center at point A we solve for force RBD as

=>

=>

Now, we can solve for the remaining reaction forces. Using the equilibrium of forces in x,y directions in beam ABC, we find

=>

=>

=>

=>

Next, we use the equilibrium of forces in x,y directions in beam DEF to find

=>

=>

=>

=>

Verification of Results: The reaction forces are shown below. We can see that the equilibrium of forces in the x direction is satisfied as RAx and RDx are equal and opposite.

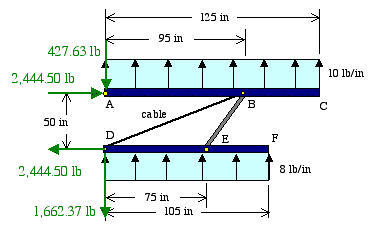
Next, we examine the summation of forces in the y direction

Finally, we check the summation of moments about point C to see if it is equal to zero.

=>

=>

With e being zero, we have confidence that there are no errors in the solution.