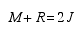
A truss is considered stable if the movements of its joints relative to each other are restrained. For a two-dimensional or planar truss consisting of M members and R support reactions, the condition of stability can be expressed mathematically as
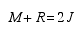 |
(1) |
where J is the number of joints in the truss. If M+ R< 2J, the truss will be unstable and will collapse under the load.
The 2J term in Eq. (1) is based on the fact that the forces acting at a given joint form a two-dimensional concurrent force system allowing the use of only two force equilibrium equations.
For space (3-dimensional) trusses, the stability criterion is given by
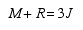 |
(2) |
Although Eqs. (1) and (2) give a quick assessment of stability, they do not provide much insight as to what it takes for a truss to be stable. The utility of these equations is in determination of whether or not a truss is statically determinate, which is the subject discussed later in this module.