Polar Moment of Inertia: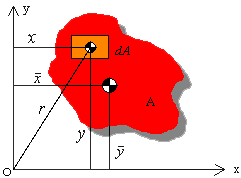
The polar moment of inertia of area A shown below about point O is
defined as
 |
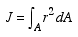(3) |
Since x and y form the rectangular components of distance r, we have the equality
Thus, the polar moment of inertia is simply the sum of Ix and Iy defined by Eqs. (1) and (2).
Application: The polar moment of inertia is used in finding the shear stress and twist angle in shafts under torsion.