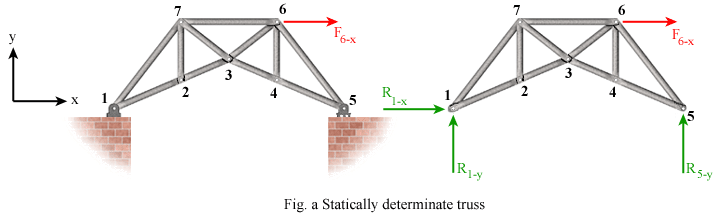
A truss is considered statically determinate if all of its support reactions and member forces can be calculated using only the equations of static equilibrium. For a planar truss to be statically determinate, the number of members plus the number of support reactions must not exceed the number of joints times 2. This condition is the same as that used previously as a stability criterion.
The truss shown in Fig. a has 11 members, 7 joints, and 3 support reactions. Since 11 + 3 = (2)(7), the truss is statically determinate.

The truss in Fig. b is the same as that in Fig. a with the exception that it is pin supported at joints 1 and 5. Therefore, there are 4 unknown reactions. The number of members plus reactions is 15, which is larger than 2 times the number of joint. Therefore, this is a statically indeterminate truss. In this case, the truss has one redundant support reaction.
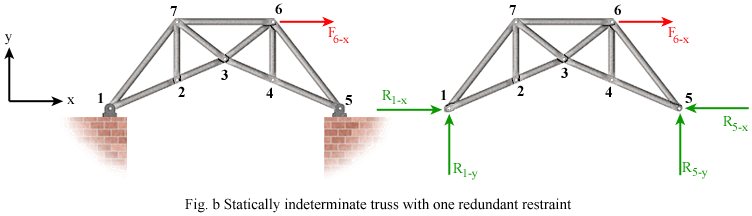
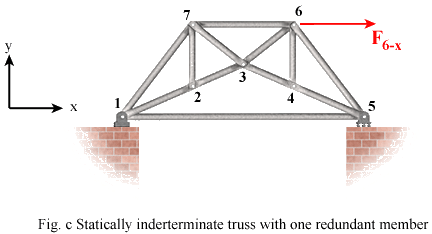
The truss in Fig. c is the same as that in Fig. a with the extra member between joints 1 and 5. 12 members plus 3 reactions is greater than 2 times the number of joints, making this a statically indeterminate truss in terms of member forces. We can solve for the reaction forces, but not the force in all the members.
Key Observation
Since a statically determinate truss cannot have more members than the number required for stability, it is not a fail-safe structure. This means that if one member of the truss were to fail, then the truss will collapse. This is a major reason for introducing redundant members in truss structures, especially when public safety is of primary concern.