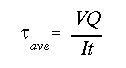
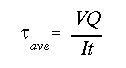
where in this case 'V' is the vertical shear force at the section, 'I' is the moment of inertia about the horizontal centroidal axis, 't' is the width of the section, and 'Q' is the first moment of area about the horizontal centroidal axis.

For the restrictions imposed on the use of this equation click here.

For this derivation we need to isolate a portion of the section. We make a horizontal cut at a distance 'y' from the horizontal centroidal axis (in this case also the neutral axis) as shown in the figure below.

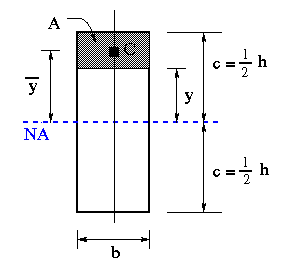
'V' force is usually a known quantity so we do the derivation in terms of V.

The moment of inertia about the horizontal centroidal axis of the rectangular cross section is

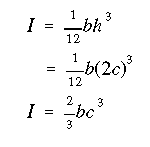
Next we write the equation for the moment of area of the shaded portion.

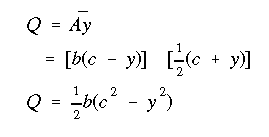
Substituting these equations into the average flexural shear stress equation we get

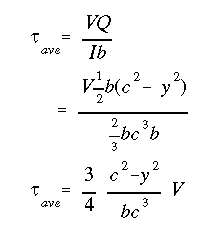
The cross sectional area of the beam is 'A=2bc', this gives the final form of the equation

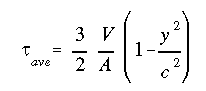
The plot of this shear stress variation is shown below.

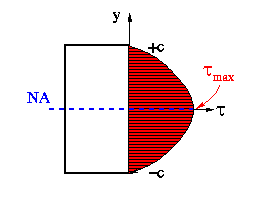
For this narrow beam, the maximum shear stress occurs at the neutral axis. Also, at the very top and bottom the shear stress is zero.

To Section III.3

To Index Page of Transverse Shear Loading of Open Sections