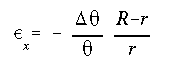
Assumptions:
a. Cross sections of the curved beam remain plane after moment is applied.
b. Material used is linearly elastic.
Restrictions:
a. Beam must have a uniform cross section along its length.
b. Beam segment considered has a constant radius of curvature.
c. Beam cross section must possess at least one axis of
symmetry so the product of inertia is zero.
d. Bending moment is applied perpendicular to
radius of curvature of the beam.
e. Bending stresses must remain below the elastic limit.
In general for beams having radii of curvature much longer than their depths, the elastic bending formula gives fairly reasonable results for bending stresses. However, for more accurate calculation of stresses especially when the radius of curvature is of the same order of magnitude as the beam's depth, then we must use Winkler's method of analysis.
In curved beams, the assumption of plane sections remain plane after loading is still valid. However, since the length of the beam varies from its top surface to the bottom surface, the strain variation is no longer linear, instead it is hyperbolic. This is evident by the equations below.
These two equations show that stress and strain vary hyperbolically along the cross section.
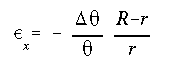
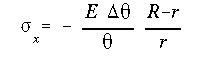
Unlike in the case of straight elastic beams, the neutral axis does not pass through the centroid of the cross section. Rather, it is located somewhere between the centroid of the cross section and the center of curvature of the beam. Its exact location can be determined by the equation given below.
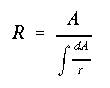
The differnetial area 'dA' is chosen in such a way that makes the evalution of the integral in the denominator fairly easy. The closed form equation for 'R' for some simple cross-sectional shapes are given in the figure below.
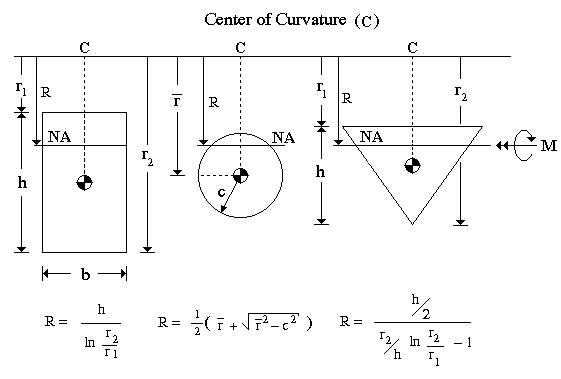
The radius of curvature, measured from the center of curvature to the centroid of the cross section, is determined by
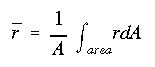
Using the moment equilibrium equation along with the Hooke's law, the bending stress in terms of moment is obtained as
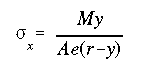 where
where
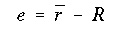
or
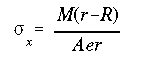
The sign associated with the moment is positive if the moment tends to increase the curvature. It is negative if it tends to decrease the curvature, or flatten the curved beam.
Strain is determined from Hooke's law as
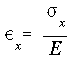
Although the stress and strain variations along the cross section of the curved beam are hyperbolic, Hooke's law is still valid because the material is linearly elastic, i.e., stress-strain relation is linear.
 To Section
II.4
To Section
II.4