Section II.4

Section II.4 Inelastic Bending of Homogeneous Beams

In this section we will first dicuss the inelastic behavior of beams in pure bending, and then elaborate on the method of analysis that we can use in such problems.

Inelastic behavior is possible in beams that are made of ductile materials, and as such can be loaded beyond the elastic limit or proportional limit of the material. This implies that the ultimate load carrying capability of a ductile beam is higher than its maximum elastic load. How much higher depends on mechanical properties of the beam material.

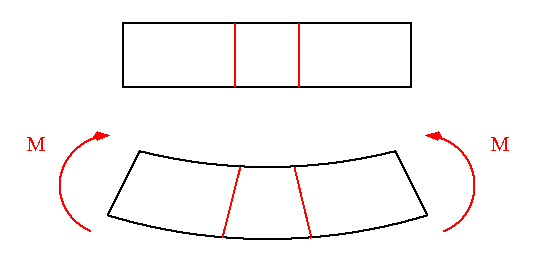
Naturally, the behavior of a beam in inelastic bending depends upon the shape of the material's stress-strain diagram. If the stress-strain diagram is known, it is possible to determine stress corresponding to a particular value of strain.

As in previous discussions we will assume that the material can be idealized as an elastoplastic material with maximum stress being the elastic limit stress, and the maximum strain being considerably higher than the elastic limit strain. It is possible for the elastoplastic material to have different characteristics in tension and in compression. For instance the corresponding elastic limit values and even the Young's moduli may be different. This tends to complicate the analysis to a certain degree.

Assumptions:
The analysis of an inelastic beam is based on the assumption that plane cross sections of a beam remain plane under pure bending, a condition that is valid for both nonlinear and linear materials. Therefore, normal strain in an inelastic beam varies linearly over the cross section of the beam.

Restrictions:
a. Beam has a symmetric cross section. It is not necessary for it to be doubly symmetric.
b. Beam is loaded symmetrically, moment is acting about either the x or the y centroidal axis.

Neutral Axis Location:
The neutral axis of beams in inelastic bending may or may not pass through the centroid of the cross section.

The following diagrams show the variations of bending strain and stress across a rectangular beam section ranging from fully elastic to fully plastic condition. Notice that the material is assumed to be elastoplastic with elastic limit in tension equal in magnitude to that in compression.

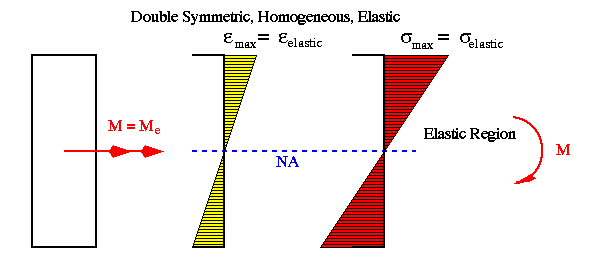
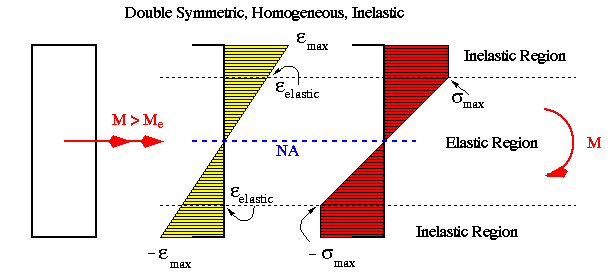
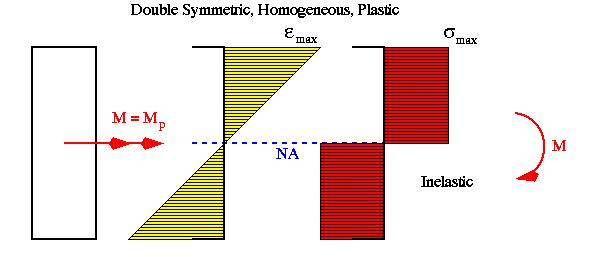
Notice that the N.A. conicides with the horizontal centroidal axis even as the beam becomes fully plastic.

If in the previous example the stress-strain variation in compression was different from that in tension, then the position of N.A. would no longer coincide with the horizontal centroidal axis as beam is loaded beyond its elastic limit.

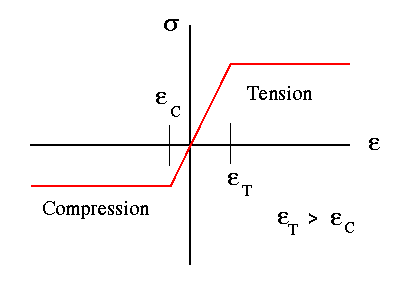
Notice that the resultant axial force is zero as the net compression force balances against the net tension force acting on the cross section.

In such beam problems, the location of N.A. coincides with the horizontal centroidal axis when the beam is elastic. However, as it is loaded beyond the elastic limit, N.A. shift either up or down relative to the centroid depending on whether the material can carry more tension or compression. The farthest position of N.A. is determined by checking the cross-sectional stress variation for a fully plastic condition.

Helpful Observations in Inelastic Bending:

1. If the stress-strain variations in tension and compression are the same, then
a. N.A. coincides with the centroidal axis (same as moment axis) if the cross section is symmetric about that axis.
b. N.A. does not conicide with the centroidal axis if the cross section is unsymmetric about that axis.

2. If the stress-strain variations in tension and compression are different, then
N.A. does not coincide with the centroidal axis regardless of cross-sectional symmetry about that axis.

Determination of a Beam's Moment Capacity:

1. Check the stress-strain variations in compression and tension. Is there a difference between elastic limit stress in tension from that in compression?

2. Is the moment acting about the axis of symmetry or not?

Case A. Moment is acting about the axis of symmetry and material properties in compression and tension are the same.

Maximum elastic moment is determined from the simplified form of Eq. (II.1)
Inelastic moment for some given value of maximum strain less than fully-plastic strain is found from the moment equilibrium equation. First determine the strain variation (remember it is linear in linearly elastic materials) across the beam. Then relate the strain variation to stress variation by checking the stress-strain diagram. Finally write the integral relating the bending moment to the stress distribution across the beam, and solve for the bending moment.
Fully-plastic bending moment is obtained by drawing the stress pattern over the beam cross section. Keep in mind that in this case the location of N.A. is the same as centroidal axis or axis of symmetry in this case. Calculate the resultant force in compression, and resultant force in tension. Sum moments about the N.A. and find the total bending moment on the beam.

Case B. Moment is acting about the axis of symmetry but material properties in compression and tension are different.

Maximum elastic moment is determined from the simplified form of Eq. (II.1).
Inelastic moment for some given value of maximum strain less than fully-plastic strain is found from the moment equilibrium equation. However, in this case the N.A. position is unknown. Therefore, an iterative solution based on a guessed position of N.A. is required. Guess a position for N.A. relative to the centroidal axis moment is acting about. From linearity of strain, determine the strain variation, then relate the strains to stresses and use the axial force equilibrium equation, and see whether the sum of forces goes to zero or not. If it goes to zero, then the location of N.A. is correct. Otherwise, guess again, and repeat the procedure. Once the location of N.A. is found, go to the moment-stress integral equation and solve for the value of moment.
Fully-plastic bending moment is obtained by drawing the stress pattern over the beam cross section. Here once again the location of N.A. is unknown. However, we know the maxium stress in compression as well as in tension. With the stress being constant in the tension side and constant in the compression side. No iteration is necessary here as the location of N.A. can be determined by summing the axial forces to zero and determining the height of compression and tension portions of the cross section. Once N.A. position is known, then proceed with determining the moment summation about the N.A. to obtain the fully-plastic bending moment.

Case C. Moment is acting about a centroidal axis which is not an axis of symmetry, and material properties in compression and tension are different. Example 1 below deals with such a problem.

EXAMPLE PROBLEMS

Example 1 Inelastic bending of a homogeneous beam section

To Section II.5

To Section II.3

To Index Page of Pure Bending