Section II.3

Section II.3 Elastic Bending of NON-Homogeneous Beams

Recall that in pure bending the normal strain variation is linear with a value of zero at the neutral axis. Before we discuss the relationship between stress and bending moment, let's first determine the location of NA. The equilibrium condition requires the sum of normal forces to go to zero. Mathematically, this is expressed as

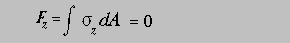
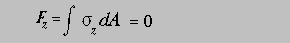
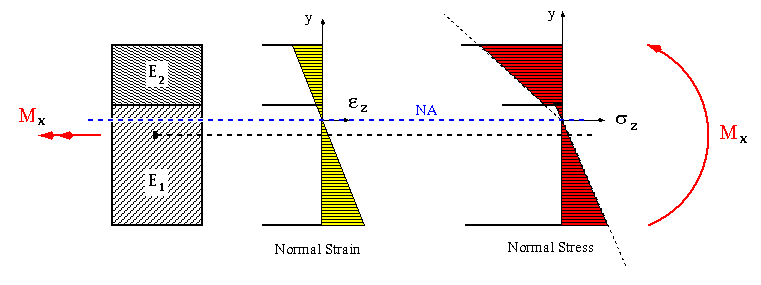
Considering a section made of two different materials with Young's moduli identified by E₁ and E₂ and with stresses below the elastic limit of each material, we can write

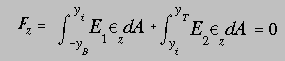
Where y_B is the distance from the NA to the bottom surface, y_i is the distance from the NA to the material interface and y_T is the distance to the top surface. Using the linear equation for strain variation gives

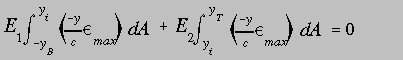
Factoring out the common terms and E₁ gives

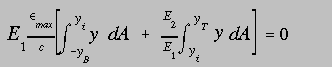
A close examination of this equation reveals that the bracketed term must be equal to zero. However, the ratio of E₂ to E₁ in front of the second term inside the brackets indicates that neutral axis will pass through the centroid of the modified homogeneous section, one with material 2 replaced with an equivalent material 1. This fact is captured in the figure below with the condition that E₂ > E₁.

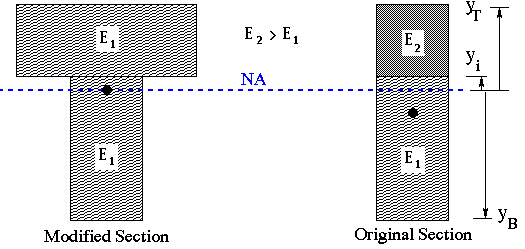
Notice that only the width of the section is modified while its height is kept the same. This condition would have been reversed if the bending moment was applied about the vertical axis.

The moment equation is written as

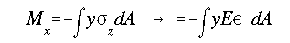
For the case of a section made of two different materials, as shown above, the integral is divided into two parts, one for each elastic material. Notice that y is measured from the neutral axis.

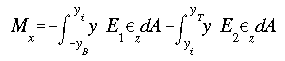
Using the linear normal strain variation we get

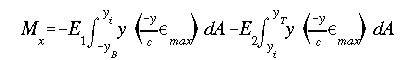
Factoring out the constant terms and normalizing with respect to E₁ we get

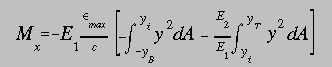
The terms inside the brackets represent the moment of inertia of the modified homogeneous section about the neutral axis, and can be expressed as

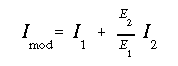
Substituting this into the previous equation and solving for the stress gives

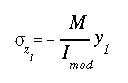
This equation can be used to calculate the bending stress only for the portion that is made of material 1. To calculate the bending stress in the portion that is made of material 2, it should be multiplied by the ratio of Young's moduli of the two materials as

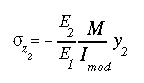
The procedure described above is known as the Modified Section Method, and is used in the analysis of elastic non-homogeneous beam sections in bending.

EXAMPLE PROBLEMS

Example 1 Design of an elastic, non-homogeneous beam under horizontal bending moment

To Section II.4

To Section II.2

To Index Page of Pure Bending