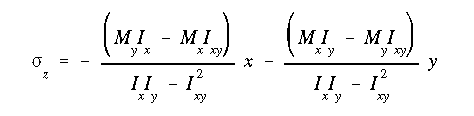 (II.1)
(II.1)
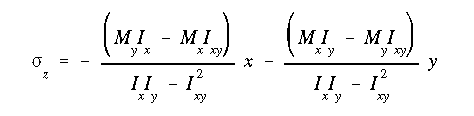 (II.1)
(II.1)
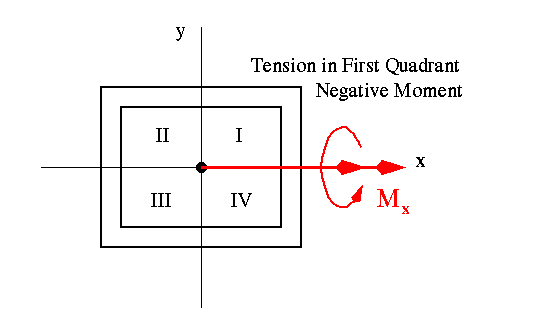
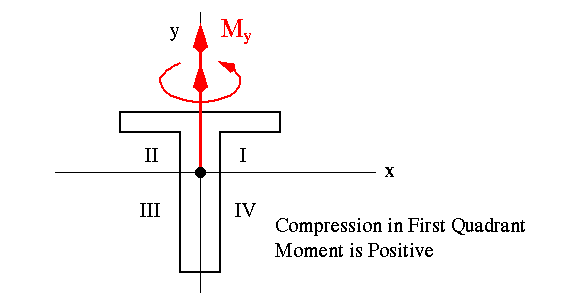
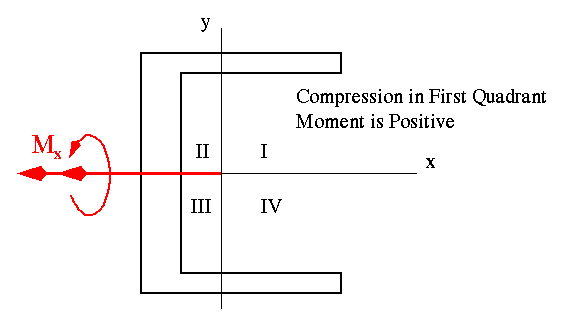
Sign Convention on Bending Moment Components Mx and My:
As far as the general bending stress equation is concerned, if a moment component puts the first quadrant of the beam cross section in compression, it is treated as positive (see the examples shown below). Notice that this is just a sign convention for the moment components and should not be confused with the sign associated with the bending stress.
Neutral Axis:
When a homogeneous beam is subjected to elastic bending, the neutral axis (NA) will pass through the centroid of its cross section, but the orientation of the NA depends on the orientation of the moment vector and the cross sectional shape of the beam.
When the loading is unsymmetrical (at an angle) as seen in the figure below, the NA will also be at some angle - NOT necessarily the same angle as the bending moment.
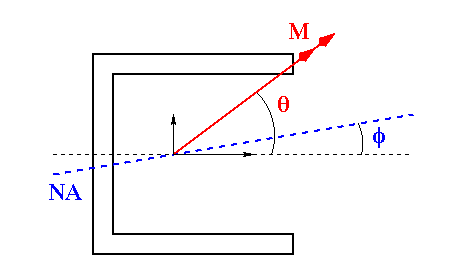
Realizing that at any point on the neutral axis, the bending strain and stress are zero, we can use the general bending stress equation to find its orientation. Setting the stress to zero and solving for the slope y/x gives
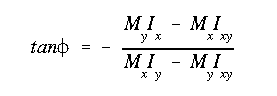 (II.2)
(II.2)A positive angle is defined as counter clockwise from the horizontal centroidal axis.
Notice that we can use the equation for orientation of NA to examine special cases. For example, if the cross section has an axis of symmetry, Ixy = 0. In addition if only Mx is applied, then NA will have angle of zero which is consistent with what we would expect from mechanics of materials.
From this equation, we see that the orientation of NA is a function of both loading condition as well as cross sectional geometry.
 To Section
II.3
To Section
II.3