Section II.2 example 2 SECTION II.2 EXAMPLE 2
For the cross section and loading shown, determine Assume that the stresses due to the applied load do not exceed the elastic limit. Also assume that each lenght shown is measured to the middle of the adjacent member.

Use the Java screen shown below to change the problem data and see the results.

EQUATIONS USED: Eq. A13.13 and Eq. A13.15

SOLUTION

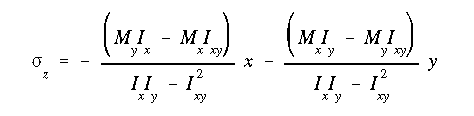
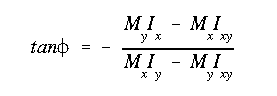
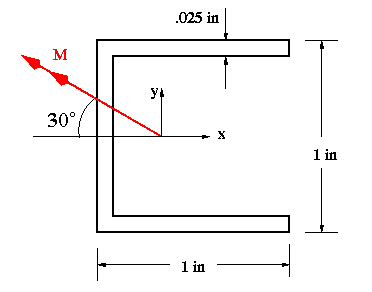
(a) As seen in the figure above, this is a symmetric cross section with unsymmetric loading. The response will be an unsymmetric bending.

With the product of inertia being zero due to cross-sectional symmetry, we need to calculate the components of the applied bending moment and the rectangular moments of inertia in order to determine the orientation of NA.

The components of bending moment are:

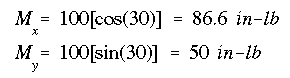
By examinning the applied moment, it is clear that both of its components will produce compression on the first quadrant, hence, they are both positive.

To calculate the rectangular moments of inertia, it is necessary to know the location of the centroid. Due to horizontal symmetry only the horizontal coordinate of centroid need to be calculated as its vertical coordinate is known due to symmetry.

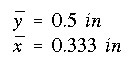
The moments of inertia about the x and y axes are

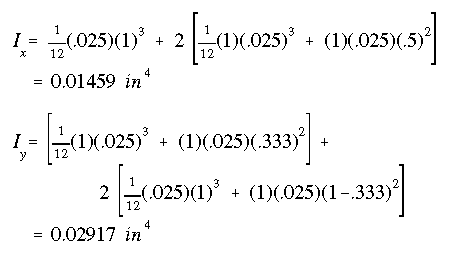
The neutral axis will pass through the centroid with an angle of

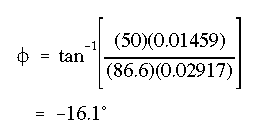
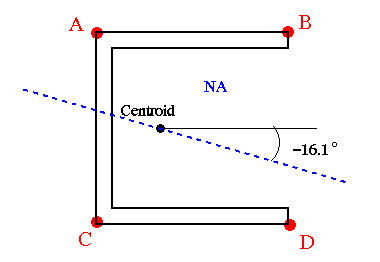
(b) The maximum axial stress is at the farthest point from the NA, either at point A, B, C, or D. To get the stress values, use equation A13.13 at all four points. With the product of inertia equal to zero A13.13 reduces to

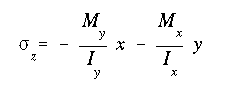
The bending stresses at point A, B, C, and D are

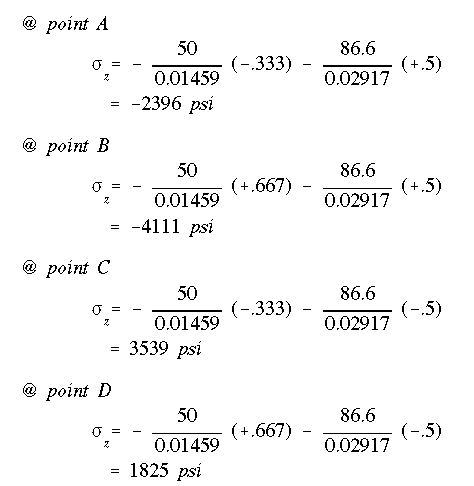
The results indicate that the maximum bending stress is at point B

To Next Example

To Section II.2

To Index Page of Pure Bending