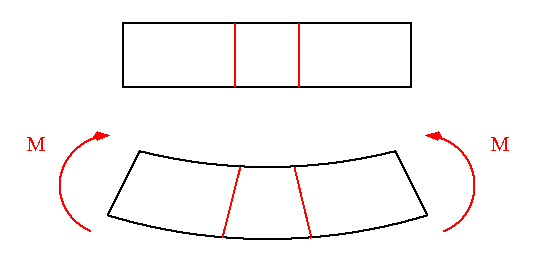

As illustrated in the figure above, the top surface of the beam is shortened due to compression, and the bottom surface is elongated due to tension - both as a result of bending moment M. By examining the figure below, it becomes apparent that at some location between the top and bottom surfaces of the beam there is a surface whose length is the same as the original length of the straight beam. This surface is neither in tension nor in compression, therefore, it is referred to as the "Neutral Surface". The intersection of the neutral surface with the plane of the beam cross section is called the "Neutral Axis".
Since the beam cross section only rotates without warping, the slope of the cross sectional plane is constant, indicating that axial deflection due to bending is linear. This finding implies that in originally-straight beams in pure bending, the axial strain must also vary linearly with zero value at the Neutral Axis.
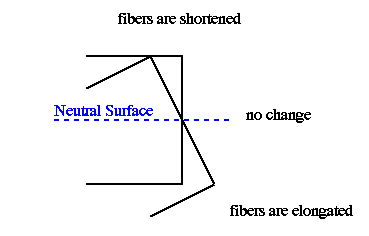
Note: The linearity of axial strain is a consequence of beam being
(a) originally straight, and
(b) in pure-bending state.
Therefore, no additional restriction such as material property or elasticity is imposed.
Now we impose additional restrictions:
(c) bending stresses remain below material's elastic stress limit,
(d) stress-strain relationship is linear.
As a result of restrictions (c) and (d), Hooke's law may be used.
In summary it can be said that in elastic and homogeneous beams, the Neutral Axis, NA always passes through the centroid of the cross section with its orientation determined according to the shape of the cross section and the orientation of the bending moment.
The stress and strain variations for some elastic beams are given below.
 To Section
II.2
To Section
II.2