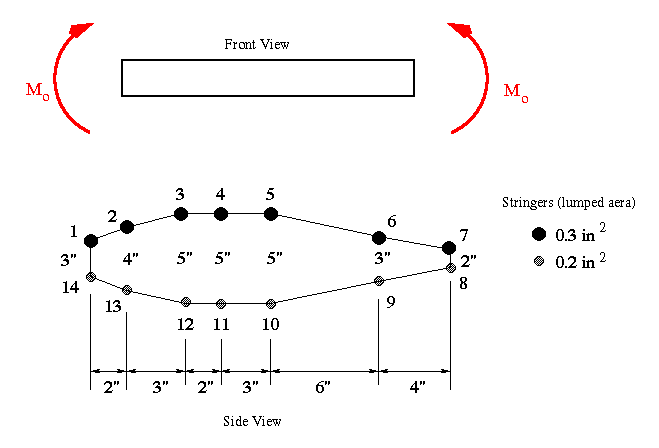

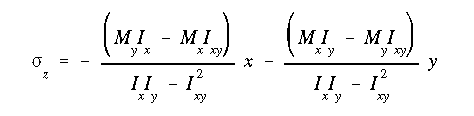
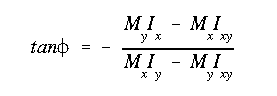
Since the cross section is not symmetric, the product of inertia will not be zero. With the reference point at stiffener 14, the centriod of this cross section is obtained first. Then the rectangular moments of inertia and product of inertia are determined.
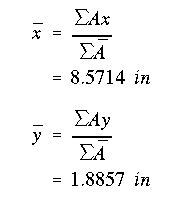
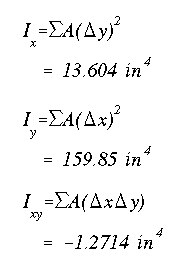
(a) Since the wing section is elastic, the NA passes through the centroid. Equation A13.15 gives
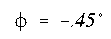
Note that Mx = Mo and My = 0 in this problem.
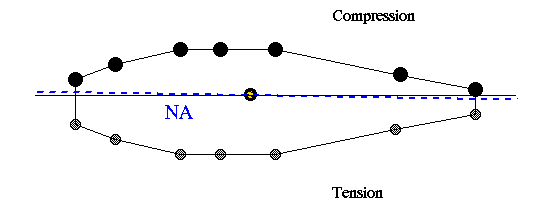
(b) The simplest way to find the largest permissible Mo is to pick out a few candidate stiffeners that appear the farthest from the NA. Then use equation A13.13 to solve for Mo by fixing the stress at 12,000 psi. The lowest moment will be the answer as it will not induce a bending stress at any point above the allowable value of 12,000 psi.
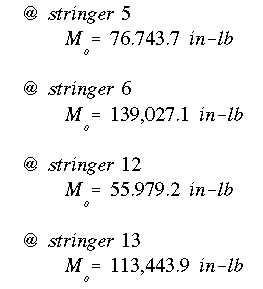
In this case, stiffener 12 will have the maximum stress because it is the farthest from the NA. Therefore, largest permissible moment is
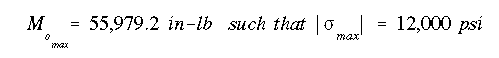
(c) Use Momax for Mx in Eq. A13.13 to solve for stress in each stiffener.

 To Previous Example
To Previous Example