Section III.2

Section III.2 Shear Center

Consider the figure below showing a cantilever beam with a transverse force at the tip. Under the action of this load, the beam may twist as it bends. It is the line of action of the lateral force that is responsible for this bend-twist coupling. If the line of action of the force passes through the Shear Center of the beam section, then the beam will only bend without any twist. Otherwise, twist will accompany bending.

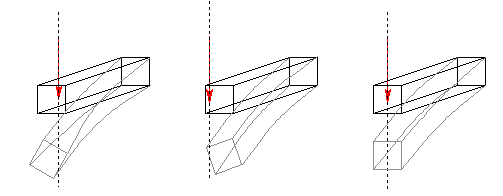
The shear center is in fact the centroid of the internal shear force system. Depending on the beam's cross-sectional shape along its length, the location of shear center may vary from section to section. A line connecting all the shear centers is called the elastic axis of the beam. When a beam is under the action of a more general lateral load system, then to prevent the beam from twisting, the load must be centered along the elastic axis of the beam.

The two following points facilitate the determination of the shear center location.

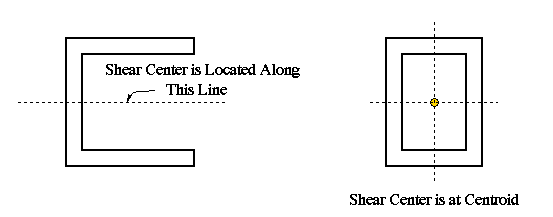
  1. The shear center always falls on a cross-sectional axis of symmetry.
  2. If the cross section contains two axes of symmetry, then the shear center is located at their intersection. Notice that this is the only case where shear center and centroid coincide.

If the cross section contains no axis of symmetry or only one axis of symmetry, the determination of the exact location of shear center requires a more detailed analysis which we will discuss in following sections.

To Section III.3

To Section III.1

To Index Page of Transverse Shear Loading of Open Sections