Section III.6

Section III.6 Analysis of Beams with Constant Shear Flow Webs

The discussions of flexural shear stress and shear flow, so far, have been focused on sections which are fully effective in bending. This means that the entire cross section was used in calculation of centroid and moments of inertia. The shear flow varied either linearly or non-linearly along each member of the cross section. As such the calculation of shear flow was somewhat involved.

In this section our focus shifts to built-up beams (with open section) that are composed of thin web(s) supported by stiffeners (or stringers). In the analysis of such beams the following assumptions are made.

Assumptions:

1. Calculations of centroid, symmetry, moments of area and moments of inertia are based totally on the areas and distribution of beam stiffeners.
2. A web does not change the shear flow between two adjacent stiffeners and as such would be in the state of constant shear flow.
3. The stiffeners carry the entire bending-induced normal stresses, while the web(s) carry the entire shear flow and corresponding shear stresses.

Analysis:

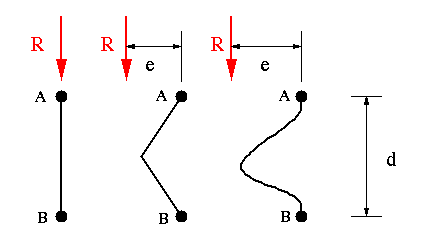
Let's begin with a simplest thin-walled stiffened beam. This means a beam with two stiffeners and a web. Such a beam can only support a transverse force that is parallel to a straight line drawn through the centroids of two stiffeners. Examples of such a beam are shown below. In these three beams, the value of shear flow would be equal although the webs have different shapes.

The reason the shear flows are equal is that the distance between two adjacent stiffeners is shown to be 'd' in all cases, and the applied force is shown to be equal to 'R' in all cases. The shear flow along the web can be determined by the following relationship

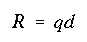
Important Features of Two-Stiffener, Single-Web Beams:

Shear flow between two adjacent stiffeners is constant.
The magnitude of the resultant shear force is only a function of the straight line between the two adjacent stiffeners, and is absolutely independent of the web shape.
The direction of the resultant shear force is parallel to the straight line connecting the adjacent stiffeners.
The location of the resultant shear force is a function of the enclosed area (between the web, the stringers at each end and the arbitrary point 'O'), and the straight distance between the adjacent stiffeners. This is the only quantity that depends on the shape of the web connecting the stiffeners.
The line of action of the resultant force passes through the shear center of the section.

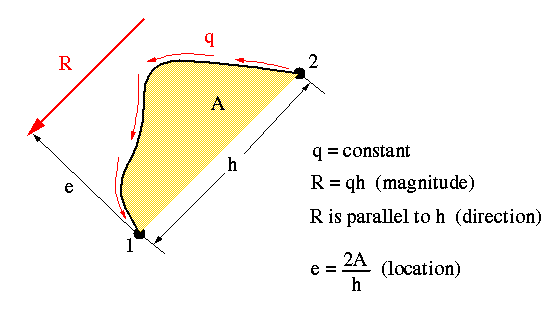
For multi-stiffener, multi-web beams the shear flow never changes direction in the web between the adjacent stiffeners. But it can change direction at a stiffener separating two adjacent webs.

EXAMPLE PROBLEMS

Example 1 Resultant shear force in a web connecting two stiffeners
Example 2 Shear flow distribution and shear center location in a multi-web multi-stiffener open section

To Section III.5

To Index Page of Transverse Shear Loading of Open Sections